There are three random variables, $x,y,z$. The three correlations between the three variables are the same. That is,
$$\rho=\textrm{cor}(x,y)=\textrm{cor}(x,z)=\textrm{cor}(y,z)$$
What is the tightest bound you can give for $\rho$?
There are three random variables, $x,y,z$. The three correlations between the three variables are the same. That is,
$$\rho=\textrm{cor}(x,y)=\textrm{cor}(x,z)=\textrm{cor}(y,z)$$
What is the tightest bound you can give for $\rho$?
The common correlation $\rho$ can have value $+1$ but not $-1$. If $\rho_{X,Y}= \rho_{X,Z}=-1$, then $\rho_{Y,Z}$ cannot equal $-1$ but is in fact $+1$. The smallest value of the common correlation of three random variables is $-\frac{1}{2}$. More generally, the minimum common correlation of $n$ random variables is $-\frac{1}{n-1}$ when, regarded as vectors, they are at the vertices of a simplex (of dimension $n-1$) in $n$-dimensional space.
Consider the variance of the sum of $n$ unit variance random variables $X_i$. We have that $$\begin{align*} \operatorname{var}\left(\sum_{i=1}^n X_i\right) &= \sum_{i=1}^n \operatorname{var}(X_i) + \sum_{i=1}^n\sum_{j\neq i}^n \operatorname{cov}(X_i,X_j)\\ &= n + \sum_{i=1}^n\sum_{j\neq i}^n \rho_{X_i,X_j}\\ &= n + n(n-1)\bar{\rho} \tag{1} \end{align*}$$ where $\bar{\rho}$ is the average value of the $\binom{n}{2}$correlation coefficients. But since $\operatorname{var}\left(\sum_i X_i\right) \geq 0$, we readily get from $(1)$ that $$\bar{\rho} \geq -\frac{1}{n-1}.$$
So, the average value of a correlation coefficient is at least $-\frac{1}{n-1}$. If all the correlation coefficients have the same value $\rho$, then their average also equals $\rho$ and so we have that $$\rho \geq -\frac{1}{n-1}.$$ Is it possible to have random variables for which the common correlation value $\rho$ equals $-\frac{1}{n-1}$? Yes. Suppose that the $X_i$ are uncorrelated unit-variance random variables and set $Y_i = X_i - \frac{1}{n}\sum_{j=1}^n X_j = X_i -\bar{X}$. Then, $E[Y_i]=0$, while $$\displaystyle \operatorname{var}(Y_i) = \left(\frac{n-1}{n}\right)^2 + (n-1)\left(\frac{1}{n}\right)^2 = \frac{n-1}{n}$$ and $$\operatorname{cov}(Y_i,Y_j) = -2\left(\frac{n-1}{n}\right)\left(\frac{1}{n}\right) + (n-2)\left(\frac{1}{n}\right)^2 = -\frac{1}{n}$$ giving $$\rho_{Y_i,Y_j} = \frac{\operatorname{cov}(Y_i,Y_j)}{\sqrt{\operatorname{var}(Y_i)\operatorname{var}(Y_j)}} =\frac{-1/n}{(n-1)/n} = -\frac{1}{n-1}.$$ Thus the $Y_i$ are random variables achieving the minimum common correlation value of $-\frac{1}{n-1}$. Note, incidentally, that $\sum_i Y_i = 0$, and so, regarded as vectors, the random variables lie in a $(n-1)$-dimensional hyperplane of $n$-dimensional space.
The tightest possible bound is $-1/2 \le \rho \le 1$. All such values can actually appear--none are impossible.
To show there is nothing especially deep or mysterious about the result, this answer first presents a completely elementary solution, requiring only the obvious fact that variances--being the expected values of squares--must be non-negative. This is followed by a general solution (which uses slightly more sophisticated algebraic facts).
The variance of any linear combination of $x,y,z$ must be non-negative. Let the variances of these variables be $\sigma^2, \tau^2,$ and $\upsilon^2$, respectively. All are nonzero (for otherwise some of the correlations would not be defined). Using the basic properties of variances we may compute
$$0 \le \text{Var}(\alpha x/\sigma + \beta y/\tau + \gamma z/\upsilon) = \alpha^2 +\beta^2+\gamma^2 + 2\rho(\alpha\beta+\beta\gamma+\gamma\alpha)$$
for all real numbers $(\alpha, \beta, \gamma)$.
Assuming $\alpha+\beta+\gamma\ne 0$, a little algebraic manipulation implies this is equivalent to
$$\frac{-\rho}{1-\rho} \le \frac{1}{3} \left(\frac{\sqrt{(\alpha^2+\beta^2+\gamma^2)/3}}{(\alpha+\beta+\gamma)/3}\right)^2.$$
The squared term on the right hand side is the ratio of two power means of $(\alpha, \beta, \gamma)$. The elementary power-mean inequality (with weights $(1/3, 1/3, 1/3)$) asserts that ratio cannot exceed $1$ (and will equal $1$ when $\alpha=\beta=\gamma\ne 0$). A little more algebra then implies
$$\rho \ge -1/2.$$
The explicit example of $n=3$ below (involving trivariate Normal variables $(x,y,z)$) shows that all such values, $-1/2 \le \rho \le 1$, actually do arise as correlations. This example uses only the definition of multivariate Normals, but otherwise invokes no results of Calculus or Linear Algebra.
Any correlation matrix is the covariance matrix of the standardized random variables, whence--like all correlation matrices--it must be positive semi-definite. Equivalently, its eigenvalues are non-negative. This imposes a simple condition on $\rho$: it must not be any less than $-1/2$ (and of course cannot exceed $1$). Conversely, any such $\rho$ actually corresponds to the correlation matrix of some trivariate distribution, proving these bounds are the tightest possible.
Consider the $n$ by $n$ correlation matrix with all off-diagonal values equal to $\rho.$ (The question concerns the case $n=3,$ but this generalization is no more difficult to analyze.) Let's call it $\mathbb{C}(\rho, n).$ By definition, $\lambda$ is an eigenvalue of provided there exists a nonzero vector $\mathbf{x}_\lambda$ such that
$$\mathbb{C}(\rho,n) \mathbf{x}_\lambda = \lambda \mathbf{x}_\lambda.$$
These eigenvalues are easy to find in the present case, because
Letting $\mathbf{1} = (1, 1, \ldots, 1)'$, compute that
$$\mathbb{C}(\rho,n)\mathbf{1} = (1+(n-1)\rho)\mathbf{1}.$$
Letting $\mathbf{y}_j = (-1, 0, \ldots, 0, 1, 0, \ldots, 0)$ with a $1$ only in the $j^\text{th}$ place (for $j = 2, 3, \ldots, n$), compute that
$$\mathbb{C}(\rho,n)\mathbf{y}_j = (1-\rho)\mathbf{y}_j.$$
Because the $n$ eigenvectors found so far span the full $n$ dimensional space (proof: an easy row reduction shows the absolute value of their determinant equals $n$, which is nonzero), they constitute a basis of all the eigenvectors. We have therefore found all the eigenvalues and determined they are either $1+(n-1)\rho$ or $1-\rho$ (the latter with multiplicity $n-1$). In addition to the well-known inequality $-1 \le \rho \le 1$ satisfied by all correlations, non-negativity of the first eigenvalue further implies
$$\rho \ge -\frac{1}{n-1}$$
while the non-negativity of the second eigenvalue imposes no new conditions.
The implications work in both directions: provided $-1/(n-1)\le \rho \le 1,$ the matrix $\mathbb{C}(\rho, n)$ is nonnegative-definite and therefore is a valid correlation matrix. It is, for instance, the correlation matrix for a multinormal distribution. Specifically, write
$$\Sigma(\rho, n) = (1 + (n-1)\rho)\mathbb{I}_n - \frac{\rho}{(1-\rho)(1+(n-1)\rho)}\mathbf{1}\mathbf{1}'$$
for the inverse of $\mathbb{C}(\rho, n)$ when $-1/(n-1) \lt \rho \lt 1.$ For example, when $n=3$
$$\color{gray}{\Sigma(\rho, 3) = \frac{1}{(1-\rho)(1+2\rho)} \left( \begin{array}{ccc} \rho +1 & -\rho & -\rho \\ -\rho & \rho +1 & -\rho \\ -\rho & -\rho & \rho +1 \\ \end{array} \right)}.$$
Let the vector of random variables $(X_1, X_2, \ldots, X_n)$ have distribution function
$$f_{\rho, n}(\mathbf{x}) = \frac{\exp\left(-\frac{1}{2}\mathbf{x}\Sigma(\rho, n)\mathbf{x}'\right)}{(2\pi)^{n/2}\left((1-\rho)^{n-1}(1+(n-1)\rho)\right)^{1/2}}$$
where $\mathbf{x} = (x_1, x_2, \ldots, x_n)$. For example, when $n=3$ this equals
$$\color{gray}{\frac{1}{\sqrt{(2\pi)^{3}(1-\rho)^2(1+2\rho)}} \exp\left(-\frac{(1+\rho)(x^2+y^2+z^2) - 2\rho(xy+yz+zx)}{2(1-\rho)(1+2\rho)}\right)}.$$
The correlation matrix for these $n$ random variables is $\mathbb{C}(\rho, n).$
Contours of the density functions $f_{\rho,3}.$ From left to right, $\rho=-4/10, 0, 4/10, 8/10$. Note how the density shifts from being concentrated near the plane $x+y+z=0$ to being concentrated near the line $x=y=z$.
The special cases $\rho = -1/(n-1)$ and $\rho = 1$ can also be realized by degenerate distributions; I won't go into the details except to point out that in the former case the distribution can be considered supported on the hyperplane $\mathbf{x}.\mathbf{1}=0$, where it is a sum of identically distributed mean-$0$ Normal distribution, while in the latter case (perfect positive correlation) it is supported on the line generated by $\mathbf{1}'$, where it has a mean-$0$ Normal distribution.
A review of this analysis makes it clear that the correlation matrix $\mathbb{C}(-1/(n-1), n)$ has a rank of $n-1$ and $\mathbb{C}(1, n)$ has a rank of $1$ (because only one eigenvector has a nonzero eigenvalue). For $n\ge 2$, this makes the correlation matrix degenerate in either case. Otherwise, the existence of its inverse $\Sigma(\rho, n)$ proves it is nondegenerate.
Your correlation matrix is
$$ \begin{pmatrix} 1&\rho&\rho\\ \rho&1&\rho\\ \rho&\rho&1 \end{pmatrix}$$
The matrix is positive semidefinite if the leading principal minors are all non-negative. The principal minors are the determinants of the "north-west" blocks of the matrix, i.e. 1, the determinant of
$$ \begin{pmatrix} 1&\rho\\ \rho&1\end{pmatrix}$$
and the determinant of the correlation matrix itself.
1 is obviously positive, the second principal minor is $1-\rho^2$, which is nonnegative for any admissible correlation $\rho\in[-1,1]$. The determinant of the entire correlation matrix is
$$ 2\rho^3-3\rho^2+1.$$
The plot shows the determinant of the function over the range of admissible correlations $[-1,1]$.
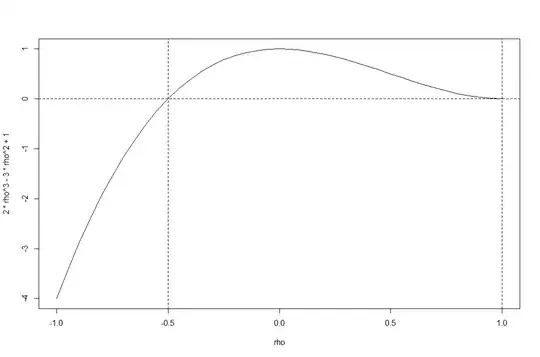
You see the function is nonnegative over the range given by @stochazesthai (which you could also check by finding the roots of the determinantal equation).
There exist random variables $X$, $Y$ and $Z$ with pairwise correlations $\rho_{XY} = \rho_{YZ} = \rho_{XZ} = \rho$ if and only if the correlation matrix is positive semidefinite. This happens only for $\rho \in [-\frac{1}{2},1]$.