(This question is from my pattern recognition course.) There is this exercise:
Imagine we have $N$ samples with $n$ dimensions.
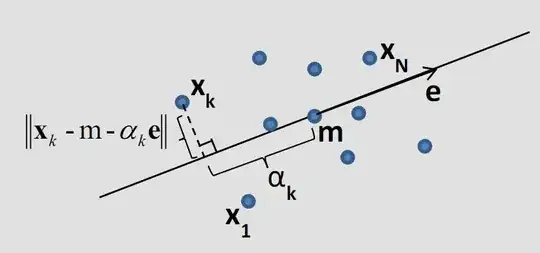
First it asks to find a point $m$ where the summation of Euclidean distances from $m$ is minimum. Then imagine another vector $e$ with size of 1. $e$ passes from $m$. Every point on this line crosses from: $x=m+\alpha*e$. The $\alpha_k$ value is the distance of a point on the line where the distance from that point and the $x_k$ is minimum. Then the exercise asks me to find values of $\alpha_k$ where the distance is minimum (i.e., the dashed line).
The last part wants me to prove that the desired values of $\alpha_k$ are actually the eigenvector with the maximum eigenvalue of the below estimation of covariance matrix: $\Sigma=1/N\sum_{k=0}^{k=N} (x-m)(x-m)^t $