3

I have the following data:

t       mean
147     1.4
143     3
137.5       1.8
133     1.9
129.5       1.8
124.5       2.5
115.5       1.9
107     2.5
102.5       6.3
98.5        6.5
94.5        5
89      5.5
81      4.8
73      9.3

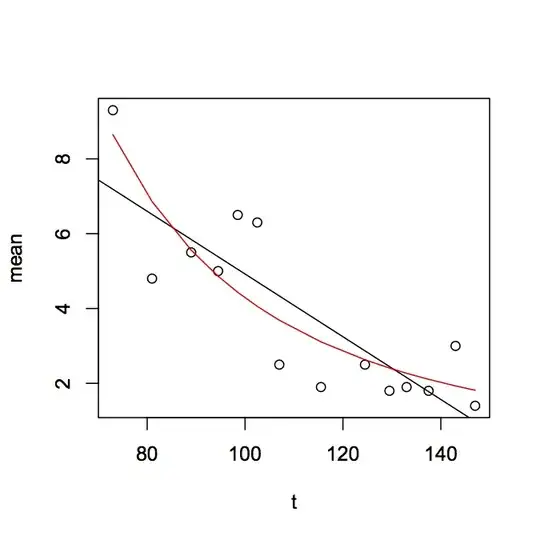
To me, the slope looks more exponential than linear when plotted as a scatterplot. I've been using the following code in R:

data<-read.csv("regression.csv")
attach(data)
plot(t,mean)
data.lm<-lm(mean~t,data=data)
summary(data.lm)
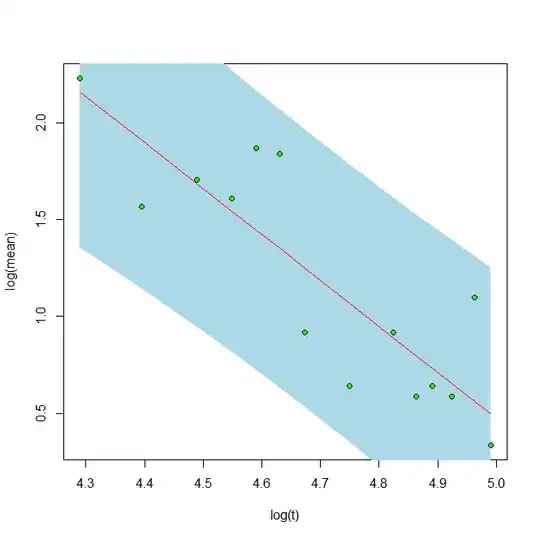
data.exp<-lm(log(mean) ~ log(t) ,data=data)
summary (data.exp)
AIC(data.lm, k=2)
AIC(data.exp, k=2)

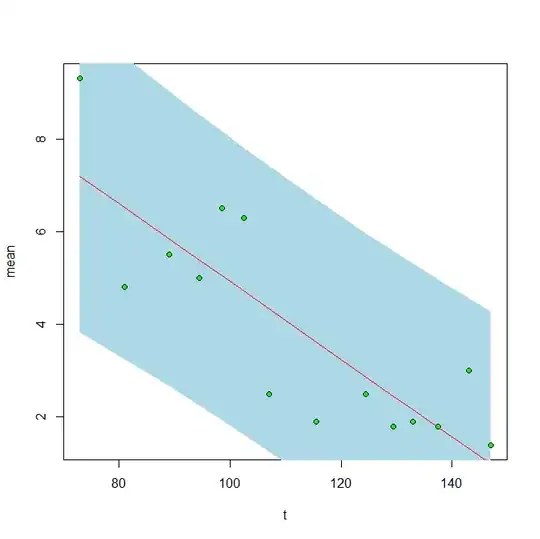
data.exp, the exponential regression, has a much lower p-value and a much lower AIC score than data.lm, the linear model: 6.869e-05 vs. 0.000194, and 11.4641 vs. 52.22926.

But (how) can I demonstrate that the data fits an exponential line better than a straight line? Is the use of AIC legitimate here? Sorry to ask such as simple question but I've looked online and haven't found an answer.

Thank you!

Charcha
  • 125
  • 1
  • 8

2 Answers2

4

There are a number of ways to approach this problem but AIC is not what you want to use the way you've done it here. The AIC is not scale invariant and once you've taken the log of your response then you're in another world.

But your best bet is to look at theory. The main reason is because exponential (and power law) relationships are locally linear. If you take a small enough piece of the curve then it will look linear. It's only when you see the whole thing that it looks exponential. So theory should guide things here more than data unless there is very clearly a shape that is obviously non-linear. Given that you feel a log-log looks best you might want to consider that the data follow a power law. Theory on that is abundant.

If you model a power law instead of taking the log-log you'll see there's not much to select between linear and the the curved model

ml <- lm(mean ~ t, data = data)
mp <- nls(mean ~ a * t ^ b, start = list(a = 1, b = 1), data = data)
plot(mean ~ t, data = data)
abline(ml)
lines(data$t, predict(mp), col = 'red')

enter image description here

Now that you've got the models of the data in the same space it's much easier to do things like compare the residuals of the two models and see which fits better. But I would be reluctant to take the small difference you'll find here as definitive evidence without some guiding theory.

John
  • 21,167
  • 9
  • 48
  • 84
2

As long as you believe in what ever model building criteria (i.e., p-values, AIC, BIC, etc.) you like, then what you are doing should be fine for comparing models (although see @John's comment for why using AIC is a bad choice). However, this does not say one model is definitively better than the other model, it simply states when compared with this criterion model A does better than model B.

Now, I plot your data and fitted the models that you did as well and honestly I am not convinced that either model does a "good" job and for that matter I do not see any evidence between the two plots that either model is doing a better job of modeling the linearity assumpotion than the other one. For example, here are my plots and the fits I obtained (also, just as a double check all my p-values and AIC values coincide with yours as well).

enter image description here enter image description here

In case you would like to reproduce these figures/results here is the code I used as well:

dat = data.frame(matrix(
c(147,1.4,
143,3,
137.5,1.8,
133,1.9,
129.5,1.8,
124.5,2.5,
115.5,1.9,
107,2.5,
102.5,6.3,
98.5,6.5,
94.5,5,
89,5.5,
81,4.8,
73,9.3),ncol=2,byrow=TRUE))

names(dat) = c("t","mean")

attach(dat)

plot(t,mean,pch=21,bg="deepskyblue")
plot(log(t),log(mean),pch=21,bg="deepskyblue")

model.lm = lm(mean~t)
model.exp = lm(log(mean)~log(t))

AIC(model.lm)
AIC(model.exp)

plot(t,mean)
polygon(c(t,rev(t)),
        c(predict(model.lm,interval="prediction")[,2],
        rev(predict(model.lm,interval="prediction")[,3])),
        col="lightblue",border=NA)
lines(t,predict(model.lm,interval="prediction")[,1],col="red")
points(t,mean,pch=21,bg="green")

plot(log(t),log(mean))
polygon(c(log(t),rev(log(t))),
        c(predict(model.exp,interval="prediction")[,2],
        rev(predict(model.exp,interval="prediction")[,3])),
        col="lightblue",border=NA)
lines(log(t),predict(model.exp,interval="prediction")[,1],col="red")
points(log(t),log(mean),pch=21,bg="green")