9

I have an example data set as follows:

Volume <- seq(1,20,0.1)
var1 <- 100 
x2 <- 1000000
x3 <- 30

x4 = sqrt(x2/pi)
H = x3 - Volume
r = (x4*H)/(H + Volume)

Power = (var1*x2)/(100*(pi*Volume/3)*(x4*x4 + x4*r + r*r))

Power <- jitter(Power, factor = 1, amount = 0.1)
plot(Volume,Power)

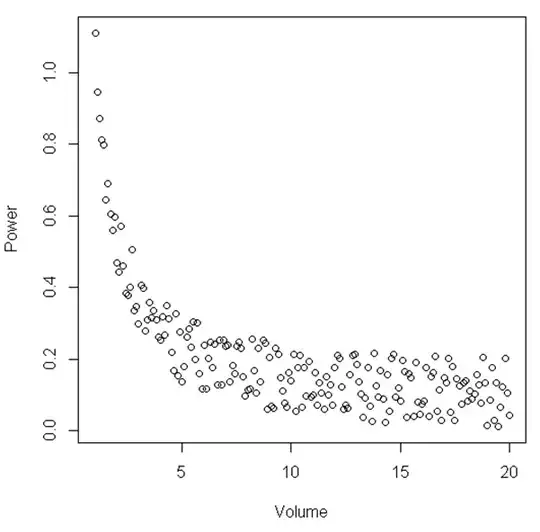
enter image description here

From the figure, it can be suggested that between a certain range of 'Volume' and 'Power' the relationship is linear, then when 'Volume' becomes relatively small the relationship becomes non-linear. Is there a statistical test for illustrating this?

With regards to some of the recommendations shown in the responses to the OP:

The example shown here is simply an example, the dataset I have looks similar to the relationship seen here although noisier. The analysis that I have conducted so far shows that when I analyse a volume of a specific liquid, the power of a signal drastically increases when there is a low volume. So, say is I only had an environment where the volume was between 15 and 20, it would almost look like a linear relationship. However, by increasing the range of points i.e. having smaller volumes, we see that the relationship is not linear at all. I am now looking for some statistical advice on how to statistically show this. Hope this makes sense.

KatyB
  • 909
  • 2
  • 12
  • 17
  • 5
    There are several things going on here. First, *of course* a relationship will look linear provided the ranges of the variables are suitably restricted. Second, the *heteroscedasticity* of the data is almost as prominent a feature as the nonlinear relationship: the scatter is greater at high volumes and low powers than it is at low volumes and high powers. Regardless, what precisely do you want to test? The linearity of the relationship across the entire range? – whuber Aug 27 '13 at 16:03
  • 4
    Actually, I would like to take back the remark about heteroscedasticity: the plot gives the *appearance* of such, but it's an illusion caused by the relatively steep slopes at lower volumes. (Volume in terms of power, though, has an extremely heteroscedastic relationship.) Once we determine that the variation in power is *not* heteroscedastic, this rules out some kinds of analyses (we would not want to apply nonlinear transformations of the power) and suggests favoring others (such as nonlinear least squares or a generalized linear model), once the nonlinearity is clearly established. – whuber Aug 27 '13 at 16:15
  • I have now added a brief description of the problem at hand. Thanks for your comments so far, these are really appreciated and are helping me think through the problem. – KatyB Aug 27 '13 at 16:18
  • Why not test for quadratic effect? – AdamO Aug 27 '13 at 16:49
  • @whuber What test did you use to see that there was no heteroscedasticity? It looks textbook to me, but I accept my knowledge may be lacking. – Simon Hayward Aug 27 '13 at 18:22
  • Kate, Consider making a [wandering schematic plot](http://stats.stackexchange.com/a/33033/919) of the raw data to see their trend, and then another plot of their residuals after fitting a line to the data (using any line-fitting technique you like, including the [three-point method](http://stats.stackexchange.com/questions/24227/how-to-choose-the-best-transformation-to-achieve-linearity/24236#24236). These graphics will provide more insight than any formal test and will clearly *show* any nonlinearities. – whuber Aug 27 '13 at 18:22
  • 2
    @Simon I did not use any test, but nevertheless you can *see* that this is homoscedastic by plotting the typical size of residuals against the Volume. Here's some `R` code: `plot(s – whuber Aug 27 '13 at 18:31
  • I'm confused by both the question *and* most of the answers here. You can see quite clearly from the code that the sample data has been generated with a single underlying curve of simple form (no straight lines involved) *and* with constant noise variance (the call to 'jitter'). Why suppose things you can immediately see cannot be true? I guess it's a good lesson for data analysis - in how easily our eyes can fool us. – Glen_b Aug 27 '13 at 23:39

3 Answers3

4

This is basically a model selection problem. I encourage you to select a set of physically-plausible models (linear, exponential, maybe a discontinuous linear relationship) and uses Akaike Information Criterion or Bayesian Information Criterion to select the best - keeping in mind the heteroscedasticity issue that @whuber points out.

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Drew Steen
  • 674
  • 6
  • 18
2

Have you tried googling this!? One way to do this is to fit higher power or other non linear terms to your model and test if their coefficients are significantly different from 0.

There's some examples here http://www.albany.edu/~po467/EPI553/Fall_2006/regression_assumptions.pdf

In your case you might want to split your data set into two sections to test for non-linearity for volume < 5 and linearity for volume > 5.

The other problem you have is that your data is heteroskedastic, which violates the normality assumption for regression data. The link provided also gives examples of testing for this.

Simon Hayward
  • 504
  • 5
  • 24
2

I suggest using nonlinear regression to fit one model to all your data. What is the point of picking an arbitrary volume and fitting one model to volumes less than that and another model to larger volumes? Is there any reason, beyond the look of the figure, for using 5 as a sharp threshold? Do you really believe that after a particular volume threshold, the ideal curve is linear? Isn't it more likely that it approaches horizontal as volume increases, but is never quite linear?

Of course, the selection of analysis tool has to depend on what scientific questions you are trying to answer and your prior knowledge of the system.

Harvey Motulsky
  • 14,903
  • 11
  • 51
  • 98