6

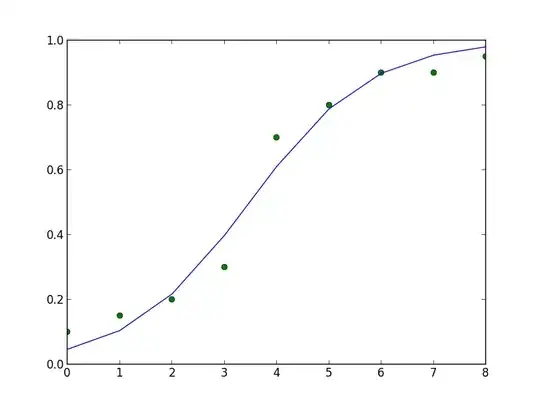
I have some 2d data that I believe is best fit by a sigmoid function. I can do the fitting with the following python code snippet. 

from scipy.optimize import curve_fit
ydata = array([0.1,0.15,0.2,0.3,0.7,0.8,0.9, 0.9, 0.95])
xdata = array(range(0,len(ydata),1))

def sigmoid(x, x0, k):
    y = 1 / (1+ np.exp(-k*(x-x0)))
    return y

popt, pcov = curve_fit(sigmoid, xdata, ydata)

However, I'd like to use a maximum likelihood approach so I can report likelihoods. I think it's possible do to this using the statsmodels package, but I can't figure it out. Any help would be appreciated.

Update:

I think the approach may be to redifine the likelihood function as it is described here:

http://statsmodels.sourceforge.net/devel/examples/generated/example_gmle.html

The plot of the above code snippet looks like this:

enter image description here

Update 2:

Here's how to do it in R:

require(bbmle)

# this sigmoid function is used to make some fake data
rsigmoid <- function(y1,y2,xi,xmid,w){
   y1+(y2-y1)/(1+exp((xmid-xi)/w))
}
counts <- round(rsigmoid(0, 1, 1:100+rnorm(100,0,3), 50, 10)*20,0)

# NOTE THAT THE SIGMOID FUNCTION IS REDEFINED AS AN R FORMULA
fit_sigmoid <- mle2(P1 ~ dbinom(prob=y1+(y2-y1)/(1+exp((xmid-xi)/w)), size=N), 
             start = list(xmid=50, w=10), 
             data=list(y1=0, y2=1, N=20, P1=counts, xi=1:100),
             method="L-BFGS-B", lower=c(xmid=1,w=1e-5), upper=c(xmid=100,w=100))
amoeba
  • 93,463
  • 28
  • 275
  • 317
Nick Crawford
  • 363
  • 1
  • 3
  • 7
  • This answer suggests a way I might do it (with some modifications) in R, but I'd like to keep everything in python if possible: http://stats.stackexchange.com/questions/31934/maximum-likelihood-estimation-of-inverse-gamma-distribution-in-r-or-rpy – Nick Crawford Aug 01 '13 at 03:20

1 Answers1

10

Here's some pseudocode to do it. Of course, it depends on the error structure you choose. You don't need the stats models to do it, because Scipy has an minimizer built-in. The minimizer probably doesn't give you CIs though, like mle2 will. There may be another minimizer that will profile your parameters, but I don't know of one on the top of my head.

Anyway, here you go

from scipy import stats
import numpy as np
from scipy.optimize import minimize
import pylab as py

ydata = np.array([0.1,0.15,0.2,0.3,0.7,0.8,0.9, 0.9, 0.95])
xdata = np.array(range(0,len(ydata),1))

def sigmoid(params):
    k = params[0]
    x0 = params[1]   
    sd = params[2]

    yPred = 1 / (1+ np.exp(-k*(xdata-x0)))

    # Calculate negative log likelihood
    LL = -np.sum( stats.norm.logpdf(ydata, loc=yPred, scale=sd ) )

    return(LL)


initParams = [1, 1, 1]

results = minimize(sigmoid, initParams, method='Nelder-Mead')
print results.x

estParms = results.x
yOut = yPred = 1 / (1+ np.exp(-estParms[0]*(xdata-estParms[1])))

py.clf()
py.plot(xdata,ydata, 'go')
py.plot(xdata, yOut)
py.show()

This gives me the following: MLfit

Nate
  • 768
  • 5
  • 10
  • This is close, but ideally I'd like to use a binomial not a normal distribution. – Nick Crawford Aug 23 '13 at 17:37
  • You can specify whatever family you want. Just change stats.norm.logpdf to stats.binom.logpmf and make the appropriate changes to your argument and that should do it. – Nate Aug 24 '13 at 14:06