2

I stumbled around this piece of code:

v1 <- eigen(X.center %*% t(X.center))$vectors[,1]

X.0 <- v1 %*% t(v1) %*% X.center

while v1 is the eigenvector corresponding to the highest eigenvalue,v1%*%t(v1) gives the outer product of v1, what X.0 signifies then and what is its physical significance? And I guess this is not a quadratic form. Can somebody point to some relevant examples please.

Thanks in advance.

bjou
  • 255
  • 1
  • 3
  • 15
The August
  • 289
  • 1
  • 3
  • 11
  • In order to assign physical significance to the formula above, I would think you need to give some sort of physical meaning to your data. No, X.0 is not a quadratic form. Geometrically, the matrix $v1 %*% t(v1)$ is a rank 1 matrix that spans the column space of $v1$. Knowing what $X.center$ is might help expand this line of thought. – caburke Jun 25 '13 at 17:21
  • The X.center matrix was derived by subtracting the column mean from each values of that column, and X is the original data matrix X.mean – The August Jun 25 '13 at 18:02

1 Answers1

4

Geometrically, whenever $v_1$ is a unit (column) vector, left multiplication of any column vector $x$ by v1 %*% t(v1) (which is $v_1 \cdot v_1'$) is the projection of $x$ onto $v_1$. In this application, $v_1$ is the first principal component of a centered matrix of columns. Therefore, this code computes the projection of the centered columns onto their first principal component.

Continuing the illustrations at Bottom to top explanation of the Mahalanobis distance?, which describes this procedure in more detail, we may depict it in the two-column situation as starting with

Start

and, after finding the center and principal axis of these points as described there, doing this:

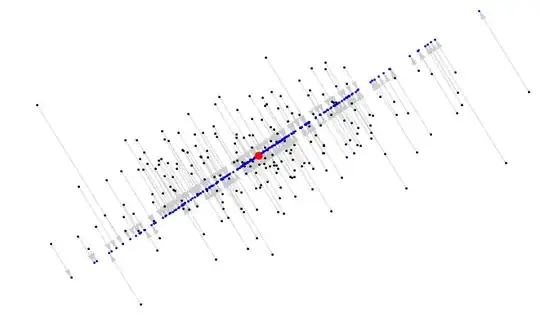
Finish

The gray arrows depict the process of (orthogonal) projection; the blue points are the results of this projection. They all lie along the principal axis and everything is done using the point of averages (in red) as the origin. A similar illustration appears at the end of JD Long's explanation of Principal Components Analysis (PCA) at https://stats.stackexchange.com/a/2700.

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101