10

The situation

I have a dataset with one dependent $y$ and one independent variable $x$. I want to fit a continuous piecewise linear regression with $k$ known/fixed breakpoints occurring at $(a_{1}, a_{2}, \ldots, a_{k})$. The breakpoins are known without uncertainty, so I don't want to estimate them. Then I fit a regression (OLS) of the form $$ y_{i} = \beta_{0} + \beta_{1}x_{i} + \beta_{2}\operatorname{max}(x_{i}-a_{1},0) + \beta_{3}\operatorname{max}(x_{i}-a_{2},0) +\ldots+ \beta_{k+1}\operatorname{max}(x_{i}-a_{k},0) +\epsilon_{i} $$ Here is an example in R

set.seed(123)
x <- c(1:10, 13:22)
y <- numeric(20)
y[1:10] <- 20:11 + rnorm(10, 0, 1.5)
y[11:20] <- seq(11, 15, len=10) + rnorm(10, 0, 2)

Let's assume that the breakpoint $k_1$ occurs at $9.6$:

mod <- lm(y~x+I(pmax(x-9.6, 0)))
summary(mod)

Coefficients:
                    Estimate Std. Error t value Pr(>|t|)    
(Intercept)          21.7057     1.1726  18.511 1.06e-12 ***
x                    -1.1003     0.1788  -6.155 1.06e-05 ***
I(pmax(x - 9.6, 0))   1.3760     0.2688   5.120 8.54e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

The intercept and slope of the two segments are: $21.7$ and $-1.1$ for the first and $8.5$ and $0.27$ for the second, respectively.

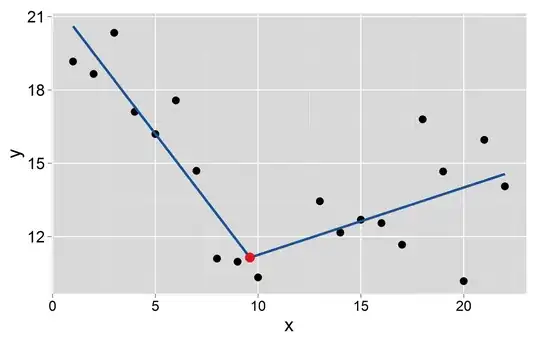
Breakpoint

Questions

  1. How to easily calculate the intercept and slope of each segment? Can the model be reparemetrized to do this in one calculation?
  2. How to calculate the standard error of each slope of each segment?
  3. How to test whether two adjacent slopes have the same slopes (i.e. whether the breakpoint can be omitted)?
Glen_b
  • 257,508
  • 32
  • 553
  • 939
COOLSerdash
  • 25,317
  • 8
  • 73
  • 123

2 Answers2

8
  1. How to easily calculate the intercept and slope of each segment?

The slope of each segment is calculated by simply adding all the coefficients up to the current position. So the slope estimate at $x=15$ is $-1.1003 + 1.3760 = 0.2757\,$.

The intercept is a little harder, but it's a linear combination of coefficients (involving the knots).

In your example, the second line meets the first at $x=9.6$, so the red point is on the first line at $21.7057 -1.1003 \times 9.6 = 11.1428$. Since the second line passes through the point $(9.6, 11.428)$ with slope $0.2757$, its intercept is $11.1428 - 0.2757 \times 9.6 = 8.496$. Of course, you can put those steps together and it simplifies right down to the intercept for the second segment = $\beta_0 - \beta_2 k_1 = 21.7057 - 1.3760 \times 9.6$.

Can the model be reparameterized to do this in one calculation?

Well, yes, but it's probably easier in general to just compute it from the model.

2. How to calculate the standard error of each slope of each segment?

Since the estimate is a linear combination of regression coefficients $a^\top\hat\beta$, where $a$ consists of 1's and 0s, the variance is $a^\top\text{Var}(\hat\beta)a$. The standard error is the square root of that sum of variance and covariance terms.

e.g. in your example, the standard error of the slope of the second segment is:

Sb <- vcov(mod)[2:3,2:3]
sqrt(sum(Sb))

alternatively in matrix form:

Sb <- vcov(mod)
a <- matrix(c(0,1,1),nr=3)
sqrt(t(a) %*% Sb %*% a)

3. How to test whether two adjacent slopes have the same slopes (i.e. whether the breakpoint can be omitted)?

This is tested by looking at the coefficient in the table of that segment. See this line:

I(pmax(x - 9.6, 0))   1.3760     0.2688   5.120 8.54e-05 ***

That's the change in slope at 9.6. If that change is different from 0, the two slopes aren't the same. So the p-value for a test that the second segment has the same slope as the first is right at the end of that line.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • (+1) Thanks Glen for your answer. Just one little question regarding #2: In my example, I would need the variance-covariance matrix of `x` and `I(pmax(x-9.6,0))`, is that correct? – COOLSerdash Jun 15 '13 at 08:53
  • No. I've edited an explicit example based off your example. If you'd like more details, please ask. – Glen_b Jun 15 '13 at 09:08
  • Thanks very much for the edit, that clarifies it quite a bit for me. So do I understand that correctly: the standard error is the same for each slope? – COOLSerdash Jun 15 '13 at 09:11
  • 1
    No. The procedure is the same but the value isn't. The standard error of the slope of the first segment is in your regression table (0.1788). The standard error of the second segment's slope is 0.1160. If we had a third segment, it would involve more variance-covariance terms in its sum (before the square root is taken). – Glen_b Jun 15 '13 at 09:15
6

My naive approach, which answers question 1:

mod2 <- lm(y~I((x<9.6)*x)+as.numeric((x<9.6))+
             I((x>=9.6)*x)+as.numeric((x>=9.6))-1)
summary(mod2)

#                        Estimate Std. Error t value Pr(>|t|)    
# I((x < 9.6) * x)        -1.1040     0.2328  -4.743 0.000221 ***
# as.numeric((x < 9.6))   21.7188     1.3099  16.580 1.69e-11 ***
# I((x >= 9.6) * x)        0.2731     0.1560   1.751 0.099144 .  
# as.numeric((x >= 9.6))   8.5442     2.6790   3.189 0.005704 **

But I'm not sure if the statistics (in particular degrees of freedom) are done correctly, if you do it this way.

Roland
  • 5,758
  • 1
  • 28
  • 60
  • (+1) Thank you very much for your answer. It provides a very convenient way to directly compute the intercepts and slopes, thanks! – COOLSerdash Jun 15 '13 at 08:58