2

I have fitted a certain ARMA model and got the following output:

sp

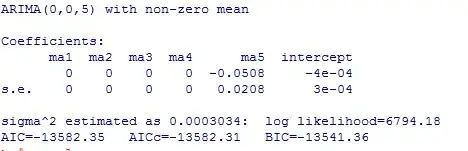
As you can see, some coeff were set to zero and the focus is on the ma5 coeff and the intercept. To be exactly, the ma5 coeff is -0.05077979 and the intercept is -0.00044509. Also the exact s.e. are 0.02078887 (ma5) and 0.00032599 (intercept). I want to calculate the p-values:

From the answer with 7 thumbs up on this thread (from mpiktas) I calculated it with:

(1-pnorm(abs(-0.05077979)/sqrt(0.02078887^2)))/2

which should give me the p-value for the ma5 coeff, and the output is

0.003645037

For the intercept I do

(1-pnorm(abs(-0.00044509)/sqrt(0.00032599^2)))/2

and get

 0.04303588

Now I control this via coeff test of the lmtest package:

library(lmtest)
coeftest(myarmamodel)

and I get

ot

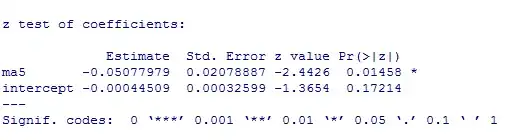
As you can see, the estimates and the s.e. are the same, but the p-value is different. My question is: Why? What is wrong? Is the p-value of the lmtest wrong or the solution in the other post?

Community
  • 1
Stat Tistician
  • 2,113
  • 4
  • 29
  • 54

1 Answers1

3

So the $z$-value in lmtest is simply the ratio of the estimate and its corresponding standard error. This is exactly what mpiktas described in the post that you linked (the one with 7 thumbs up). So, for example: $z_{ma5}=-0.05078/0.02079 = -2.443$. Then, the CDF of the standard normal distribution is used to calculate the two-sided p-value:

2*pnorm(-2.443) = 0.0146

or if you use the other/upper tail of the distribution

2*(1-pnorm(2.443)) = 0.0146

which is the p-value provided by lmtest. The solution of lmtest is straightforward and well-known, so nothing wrong with that.

I honestly don't know why mpiktas divides the value by 2 instead of multiplying it, which seems to be the correct way (EDIT: it was a mistake. Fixed in the original answer of mpiktas).

Your caluclated p-values by the method of mpiktas are therefore 4 times smaller than the ones calculated by lmtest: 4*0.003645037 = 0.0146.

COOLSerdash
  • 25,317
  • 8
  • 73
  • 123