0

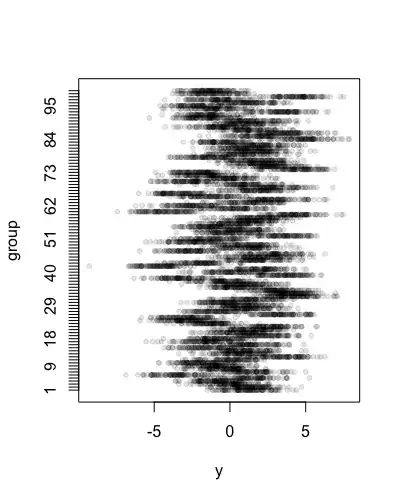
I want to do a multiple linear regression but I do not find any way to normalize the data I have. This is the distribution without transformation.

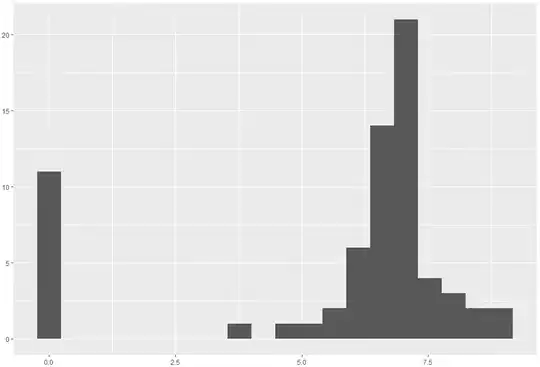
enter image description here

The data contains a good number of zeros. When I transformed them summing 1 and then taking the logarithm, I obtained this result:

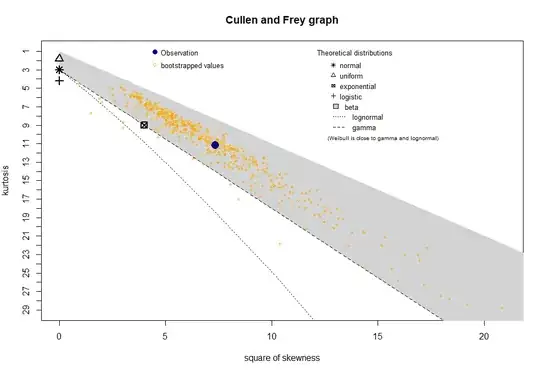
enter image description here

I also thought about using generalized linear models, but when I used

`descdist(data$variable, discrete = FALSE,boot=500)`

I obtained, the following graph, which I assume suggests the data follow a beta distribution, for which there are no glms for what I heard. Any suggestions? Thank you!!

enter image description here

Statistiasis
  • 1
  • 2
    The data does not need to be normal distributed https://stats.stackexchange.com/questions/342759/where-does-the-misconception-that-y-must-be-normally-distributed-come-from – Sextus Empiricus Feb 12 '22 at 12:30
  • A few comments... For multiple regression you don't need the ***data*** to be normally distributed, but you may want to assess the conditional distribution; that is, the residuals of the model you are fitting... beta regression is available (e.g. *betareg* package in R), but it doesn't seem appropriate for your data. If you are considering ***generalized*** linear models, you might look at Gamma regression.... If you want to force a vector of numbers to a normal distribution, *inverse normal scores transformation* is usually pretty successful, but not very useful in too many situations. – Sal Mangiafico Feb 12 '22 at 13:01

2 Answers2

0

This is an ideal situation for using a semiparametric ordinal response model such as the proportional odds model. This subsumes as a special case the well-loved Wilcoxon and Kruskal-Wallis nonparametric rank tests. Semiparametric models allow for bimodality, arbitrarily large clumping at zero, and floor and ceiling effects. No assumption is made about the shape of the reference distribution. Outliers are not allowed to have extreme influence. For an introduction to these models see the nonparametric chapter of BBR and for detail background and a case study see the chapter on ordinal models for continuous Y in the RMS course notes.

Semiparametric models are Y-transformation invariant, i.e., you get the same regression coefficients, standard errors, and p-values if you used such a model to analyze log(Y) as you get when analyzing Y.

Frank Harrell
  • 74,029
  • 5
  • 148
  • 322
0

Have a look at zero inflated lognormal regression. This is a particularly useful setup for life time value predictions. See https://github.com/google/lifetime_value and the references therein.

Apart from data properties alone, what does your data represent? Money, counts, ...? What is the source of structural zeros? Do you have predictors that are indicative of y=0 vs y>0?

Georg M. Goerg
  • 2,364
  • 20
  • 21