10

as I am stepping into forecasting with ARIMA models, I am trying to understand how I can improve a forecast based on ARIMA fit with seasonality and drift.

My data is the following time series ( over 3 years, with clear trend upwards and visible seasonality, which seems to be not supported by autocorrelation at lags 12, 24, 36??). 

    > bal2sum3years.ts
             Jan     Feb     Mar     Apr     May     Jun     Jul     Aug          
    2010 2540346 2139440 2218652 2176167 2287778 1861061 2000102 2560729 
    2011 3119573 2704986 2594432 2362869 2509506 2434504 2680088 2689888 
    2012 3619060 3204588 2800260 2973428 2737696 2744716 3043868 2867416 
             Sep     Oct     Nov     Dec
    2010 2232261 2394644 2468479 2816287
    2011 2480940 2699780 2760268 3206372
    2012 2951516 3119176 3032960 3738256

The model that was suggested by auto.arima(bal2sum3years.ts) gave me the following model:

    Series: bal2sum3years.ts 
    ARIMA(0,0,0)(0,1,0)[12] with drift         

    Coefficients:
              drift
          31725.567
    s.e.   2651.693

    sigma^2 estimated as 2.43e+10:  log likelihood=-321.02
    AIC=646.04   AICc=646.61   BIC=648.39

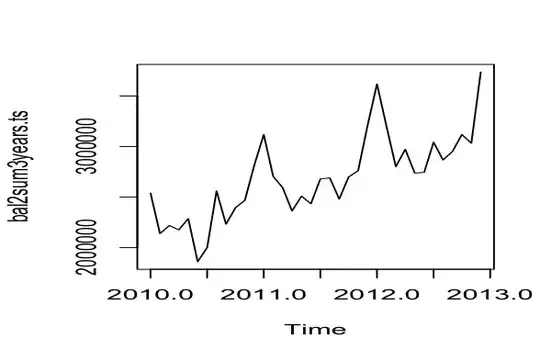
However, the acf(bal2sum3years.ts,max.lag=35) does not show acf coefficients higher than 0.3. The seasonality of the data is, however, pretty obvious - spike at the beginning of every year. This is what the series looks like on the graph: Original Time Series

The forecast using fit=Arima(bal2sum3years.ts,seasonal=list(order=c(0,1,0),period=12),include.drift=TRUE) , called by function forecast(fit), results in the next 12months's means being equal to the last 12 months of the data plus constant. This can be seen by calling plot(forecast(fit)),

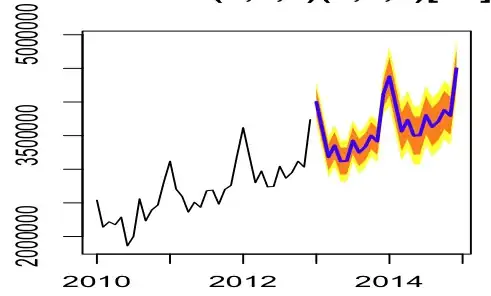
Actual and Forecasted Data

I have also checked the residuals, which are not autocorrelated but have positive mean ( non zero).

The fit does not model the original time series precisely, in my opinion ( blue the original time series, red is the fitted(fit):

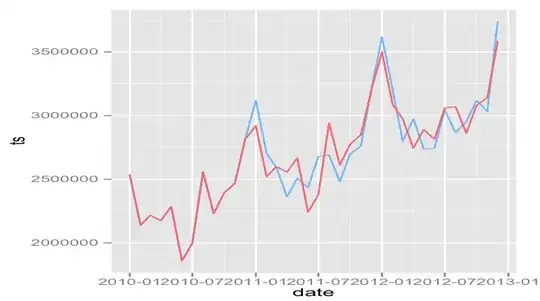
Original vs fit

The guestion is, is the model incorrect? Am I missing something? How can I improve the model? It seems that the model literally takes the last 12 months and adds a constant to achieve the next 12 months.

I am a relative beginner in time series forecasting models and statistics.

Ferdi
  • 4,882
  • 7
  • 42
  • 62
zima
  • 739
  • 3
  • 7
  • 19
  • "*The fit does not model the original time series precisely, in my opinion*" -- why would you expect it to?? – Glen_b Apr 18 '13 at 07:19
  • @Glen_b, this opinion was based on the differences that I see when I look at the plot. If I am trying to forecast, for instance, monthly sales for accounting purposes, the error could be significant... – zima Apr 18 '13 at 15:27
  • "*the differences I see when I look at the plot*" is another way of saying "*does not model the time series precisely*". This is not in dispute. Your expression of a desire for a better forecast is the same desire every forecaster has. In many cases it can be very important. Nevertheless, this desire doesn't put more information into the data. Every ARIMA model - indeed, any time series model of relevance to this task - has a nonzero error term. There will *always* be mismatch between data and fit. Is there something that makes you think your model has missed something that can be modeled? – Glen_b Apr 18 '13 at 21:37
  • I have just thought about something.. Maybe ARIMA model is indeed not able to reflect the data due to not taking into account the nature of the data - user activity on the website. I think there might be other events affecting the numbers, not just seasonality - such as special events, promotions.. Maybe other prediction methods (not ARIMA), but more complex ones involving Machine Learning techniques, are able to better predict the values. I will look into that. – zima Apr 25 '13 at 08:56
  • Quite plausible. If so, you should be able to identify such failure in the residuals. Note that both ARIMA models and structural time series models can incorporate things like special events and promotions via regression terms; time series regression models are fairly common. – Glen_b Apr 25 '13 at 09:09
  • I have checked whether the mean of the residuals is 0 (it is positive and not 0), and whether there is autocorrelation (found none). I have read that one has to add the mean to the forecast in order to account for this information hidden in the positive mean. But I am not sure how - just plain add the mean value to each forecasted value? – zima Apr 25 '13 at 09:42
  • How big was the mean of the residuals? "I have read that one has to add the mean to the forecast in order to account for this information hidden in the positive mean." - this seems odd to me. Where did you read this? – Glen_b Apr 25 '13 at 09:45
  • (http://otexts.com/fpp/2/6/), there is a sentence _"Adjust­ing for bias is easy: if the resid­u­als have mean , then sim­ply add to all fore­casts and the bias prob­lem is solved. "_. Did I misunderstand this statement? – zima May 03 '13 at 09:38
  • As a general principle that advice is great; if your procedure leaves you with a purely location-shift bias it's easily adjusted for. But my concern here is that the issue you have may not be exactly what was being gotten at in the text - your model should not have left you with a substantive bias (the residuals may not have mean exactly zero - you can get nonzero mean - but they should be quite small), assuming I have correctly understood. Anyway, if you check first it shouldn't be a problem to adjust for it - how big is the mean of the residuals? What does a plot of the residuals look like? – Glen_b May 03 '13 at 22:44

2 Answers2

9

From the appearance of your data, after seasonal differencing, there may well be no substantive remaining seasonality. That peak at the start of each year, and the subsequent pattern through the rest of the year is quite well picked up by an $I_{[12]}$ model; the model has incorporated "obvious seasonality".

Yes, indeed, the suggested model is "This June = Last June + constant + error", and similarly for the other months.

What's wrong with that exactly? It seems to be an excellent description of your data.

You might find a time-series decomposition more intuitive and easier to explain, perhaps even something based off a Basic Structural Model - one with seasonality - but that doesn't necessarily imply a model that functions better than the one you have. Still one or more of the standard decomposition techniques might be worth trying -- there's a lot to be said for a model that you comprehend well.

Glen_b
  • 257,508
  • 32
  • 553
  • 939
1

I believe that our problem is that we are jumping directly to ARIMA model without trying the traditional models. for this reason, you can find the model is not giving the needed results. In your case, I tested your data, I found that there is a seasonality every 12 months which is clear for you, but also I found that a simple moving average of 3 terms Seasonal adjustment: Multiplicative is the best model. In my opinion, We have to try the traditional forecasting algorithms before jumping to any advanced technique. 12 months forecast for question data

Awbath
  • 63
  • 6
  • 1
    The model you are suggesting is an ARIMA model of the form (3,0,0)(0,0,0) where you are hardcoding the three coefficients to be .333,.333 and .333 and a constant of 0.0 . Thus not only are assuming the form of the arima model BUT you are assuming the values of the coefficients AND no outliers exist in the series. Allow the data to speak for itself in terms of the form of the model and the optimal values for the parameters ... you have nothing to lose and a lot to gain. If indeed your model is correct then it will be found.. All arima models are weighted functions of the past. – IrishStat Nov 28 '19 at 13:11
  • 1
    https://stats.stackexchange.com/questions/40905/arima-model-interpretation/63022#63 spells out how weighted modelling and arima are related.In this way an ARIMA model can be explained as the answer to the question How many historical values should I use to compute a weighted sum of the past? Precisely what are those values? – IrishStat Nov 28 '19 at 16:48