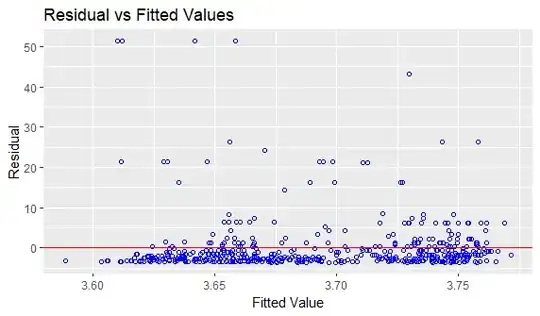
So I am pretty confused. I want to create a GLM and I dont know what distribution my residuals have in order to fit the regression model. I created a Cullen-Frey-Graph that says I have a beta distribution. When I analyse the residuals of the model however, it looks like I have a positive skewness hinting to a Gamma distribution. My response variable is percentage weed coverage and it contains a lot of very small numbers. So which is it?
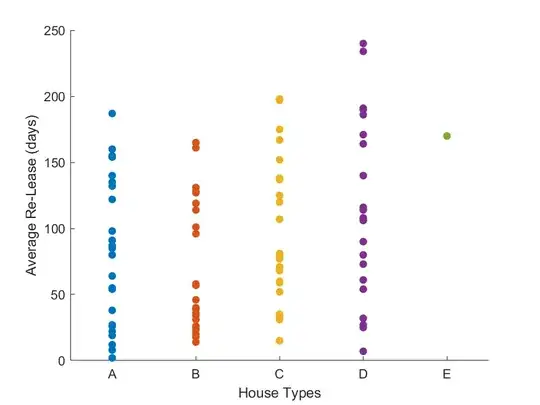
Edit: I also a scatterplot to show the Y ~ X relation