Are there any problems that are particularly well suited for models from the field of Functional Data Analysis (FDA)? I was reading the Wikipedia page for Functional Data Analysis (https://en.wikipedia.org/wiki/Functional_data_analysis), and this field is described as "a branch of statistics that analyzes data providing information about curves, surfaces or anything else varying over a continuum."
Reading this description, this seems to be very similar to regression models (e.g. splines, gaussian process regression, arima, smoothing, etc.). For instance, when looking at some of the models from the field of Functional Data Analysis:
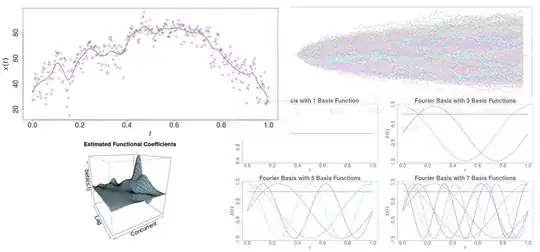
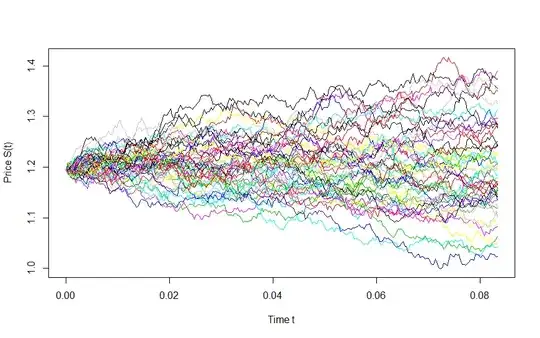
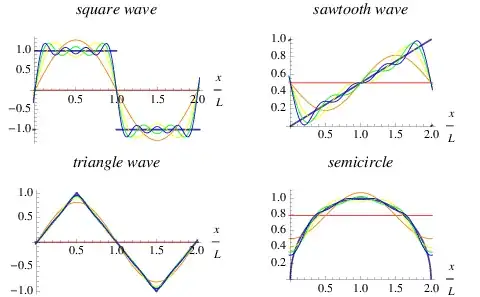
When looking at some of these images, these images look similar to models from other fields in statistics. For example:
- Brownian Motion:
- Regression Surface Modelling:
- Fourier Approximation
My question: How exactly is Functional Data Analysis different from these fields listed above? Or are all these fields included within the field of Functional Data Analysis (e.g. any statistical model can be thought of as a "function", therefore all statistical models are under the umbrella of Functional Data Analysis)? Are there any "classic examples" of Functional Data Analysis models? Are there any types of problems which particularly "require" models from Functional Data Analysis (e.g. censored event data is particularly well modelled by Survival Analysis models)?
References: