There is a standard relationship between the probability distribution function and the cumulative probability distribution function of a random variable :
We can obtain the cumulative probability distribution function by taking the integral of the probability distribution function.
We can obtain the probability distribution function by differentiating the cumulative probability distribution function.
However, I am interested in knowing if these relationships hold in the case of empirical probability distribution functions (i.e. non-smooth functions which do not have clear definitions of derivatives and integrals). I will illustrate my question using the R programming language.
Suppose I measure the weight (lbs) of 100 students:
set.seed(123)
weight = rnorm(100, 200,10)
weight
weight
[1] 194.3952 197.6982 215.5871 200.7051 201.2929 217.1506 204.6092 187.3494 193.1315 195.5434 212.2408 203.5981 204.0077 201.1068 194.4416 217.8691 204.9785
[18] 180.3338 207.0136 195.2721 189.3218 197.8203 189.7400 192.7111 193.7496 183.1331 208.3779 201.5337 188.6186 212.5381 204.2646 197.0493 208.9513 208.7813
[35] 208.2158 206.8864 205.5392 199.3809 196.9404 196.1953 193.0529 197.9208 187.3460 221.6896 212.0796 188.7689 195.9712 195.3334 207.7997 199.1663 202.5332
[52] 199.7145 199.5713 213.6860 197.7423 215.1647 184.5125 205.8461 201.2385 202.1594 203.7964 194.9768 196.6679 189.8142 189.2821 203.0353 204.4821 200.5300
[69] 209.2227 220.5008 195.0897 176.9083 210.0574 192.9080 193.1199 210.2557 197.1523 187.7928 201.8130 198.6111 200.0576 203.8528 196.2934 206.4438 197.7951
[86] 203.3178 210.9684 204.3518 196.7407 211.4881 209.9350 205.4840 202.3873 193.7209 213.6065 193.9974 221.8733 215.3261 197.6430 189.7358
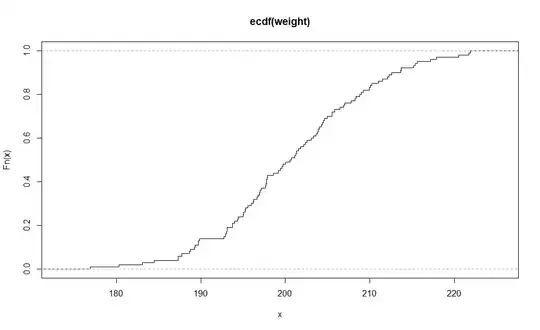
1) Based on this data, I can "calculate" the empirical probability distribution function of this data:
ecdf <- ecdf(weight)
plot(ecdf, verticals = TRUE, do.points = FALSE)
2) Using Kernel Density Estimation, I can also approximate the probability distribution function of this data:
library(ks)
fhat <- kde(x=weight, positive=TRUE)
plot(fhat, col=3)
My Question: Given some observed data, we can estimate the empirical cumulative probability distribution function and the empirical probability distribution function:
But does the same "integral-derivative" relationship hold true between both of these distributions?
Thanks!