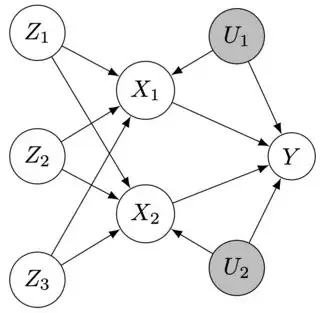
I'm interested in estimating the effects of $X_1$ and $X_2$ on $Y$ in the directed acyclic graph below. $U_1$ and $U_2$ are unobserved confounders. Based on Definition 7.4.1 on p. 248 of Causality 2nd Ed. by Pearl, $\boldsymbol Z = \{Z_1, Z_2, Z_3\}$ is not admissible as an instrumental variable for estimating the effects of $X_1$ and $X_2$ on $Y$.
This is because, for example, to estimate the effect of $X_1$ on $Y$, we need to block the path between $\boldsymbol Z$ and $Y$ by conditioning on $X_2$, but doing so opens the collider $\boldsymbol Z \rightarrow X_2 \leftarrow U_2$, violating the exclusion assumption.
Is it nevertheless appropriate to use two stage least squares (2SLS) for estimating the effects of $X_1$ and $X_2$ on $Y$ for this DAG? Are there any additional assumptions that could make this problem identifiable?