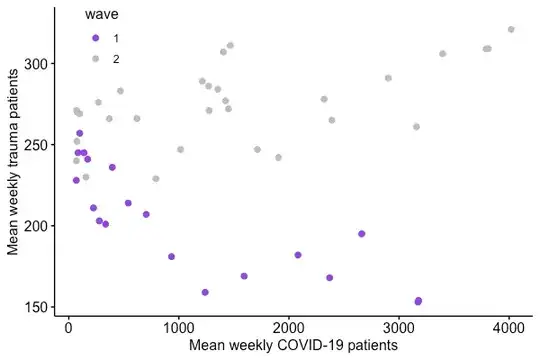
I'm trying to assess the impact of the UK government's differing approach to managing COVID-19 on healthcare outcomes. For example, I can consider weekly patients presenting with COVID-19, and weekly patients presenting following major trauma - clearly in this case there is a difference in the pattern of presentations, with a strong negative correlation during the first "wave" and a weaker positive correlation in the second:
In order to demonstrate that there is a difference between the two distributions, I can show that the correlation coefficients are different for each wave:
weekly_data %>%
group_by(wave) %>%
rstatix::cor_test(trauma, covid, method = "pearson", use = "complete.obs")
# # A tibble: 2 × 9
# wave var1 var2 cor statistic p conf.low conf.high method
# <fct> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <chr>
# 1 1 trauma covid -0.81 -5.77 0.0000227 -0.926 -0.570 Pearson
# 2 2 trauma covid 0.58 3.77 0.000775 0.278 0.778 Pearson
and subsequently use {cocor} as suggested in this answer to compare the two (treating them as independent groups):
cocor::cocor.indep.groups(r1.jk=-0.81, r2.hm=+0.58,
n1=22, n2=30,
alternative="two.sided", alpha=0.05, conf.level=0.95, null.value=0)
Is this however a statistically rigorous thing to do? I could instead model trauma as a linear model on covid and wave - would I instead report the interaction term between covid and wave, as (I think) this answer was suggesting regarding moderation and this answer regarding interactions and correlations?
summary(lm(trauma ~ covid*wave, data = weekly_data))
# ...
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 228.888354 6.547593 34.958 < 2e-16 ***
# covid -0.024666 0.004333 -5.693 8.91e-07 ***
# wave2 28.238233 8.751896 3.227 0.00234 **
# covid:wave2 0.036196 0.005289 6.843 1.74e-08 ***
Any advice on what's the most "proper" way to approach this would be much appreciated.