How do we obtain the combined level's HR or OR in a regression model?

Question

I would like to perform a cox PH model. I have identified 4 covariates to investigate the association with survival time. 2 of the covariates are trauma and workplace_injury each taking either Y or N. workplace_injury is not available for all observations, but only for trauma == "Y". Hence, those with trauma == "N" will have missing values for workplace_injury, and as a result, these observations will be removed from the model. Let's name the remaining 2 covariates as A and B to simplify.

So, I have decided to combine the 2 covariates into 1 covariate, as seen in the last column, i.e. trauma_wi.

Using "NonTrauma" as the reference on the model (A+B+trauma_wi), the result is as follows (I cropped out the results for A and B):

My first question: How do I combine the results (i.e. combine the estimates), such that I can make a comparison between Trauma (Trauma_Y and Trauma_N) and NonTrauma?

My second question: Would the results be the same if I were to run the model (A+B+trauma), i.e. ignoring the workplace_injury?

Answer 1

The potential problem with what you seek to do is that, if there is a difference between workplace_injury=="Y" and workplace_injury=="N", as there seems to be, then the value of a regression coefficient that only evaluates trauma as in your second question will depend on the relative prevalence of workplace_injury in your data sample. If outcomes are worse with workplace_injury=="Y" then the overall apparent association with trauma will be progressively worse for data samples weighted toward greater prevalence of workplace_injury=="Y".

There's nothing wrong with that in principle. If your data are representative of an underlying population and your interest is in a population-average estimate for the effect of trauma, that might be what you want. But you have to understand that and make that clear to your audience.

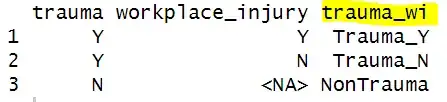
You might consider having separate predictors for trauma and workplace_injury in your model. Logically, if trauma=="N" then also workplace_Injury=="N" so you could code all your trauma=="N" cases that way. That's an accepted way to deal with situations in regression like this, when one predictor only takes non-zero values if another predictor has a non-zero value, as explained in this answer. Then you could use ANOVA to compare the nested models

model1 <- coxph(Surv(time, status)~A+B+trauma+workplace_injury

model2 <- coxph(Surv(time, status)~A+B+trauma

to evaluate the statistical significance and practical importance of workplace_injury, and proceed accordingly. The coefficients that you get from my model1 should correspond to what you have in your 3-level categorical model, with the trauma coefficient in my model1 the same as your regression coefficient for trauma_wiTrauma_N and your regression coefficient for trauma_wiTrauma_Y being the sum of the trauma and workplace_injury coefficients in my model1.* You should be able to get the same results either way, but I at least find it easier to think about the trauma and workplace_injury terms separately, particularly for evaluating the significance and importance of the different workplace_injury values.

---

*I find it best to do these types of intermediate analyses with the original (additive) coef values, rather than working with their exponentiations into multiplicative hazard ratios. You can then express the final results in terms of hazard ratios once you've added the individual coefficients appropriately.