1

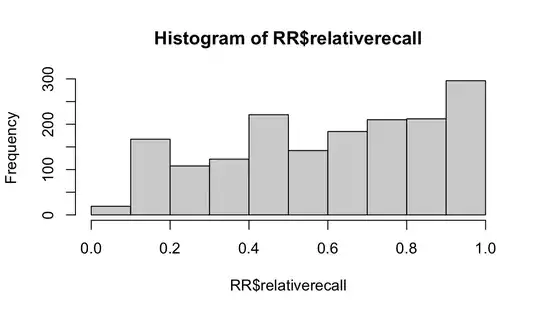
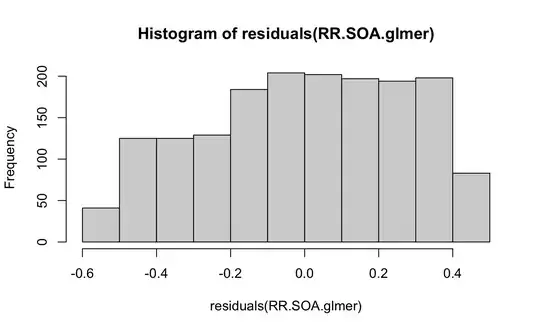
I am trying to run a glm on my DV (relative recall) which is continuous and not normally distributed: enter image description here

I am trying to predict my DV based on 2 IV and I have added subjects as a random factor. Therefore, I cannot run a non-parametric ANOVA.

Is there a way I can run a non-parametric GLM? Also, how can I determine the distribution family of these data?

I have also ran the distributions of the residuals by hist(residuals(mymodel)) which do not show a normal distribution

enter image description here

aperis
  • 13
  • 3
  • 4
    The Gaussian distribution assumption concerns the error term, not the pooled/marginal distribution of $y$. – Dave Aug 16 '21 at 17:27
  • 3
    Since your response variable appears to lie between 0 and 1, the conditional distribution of $Y$ (which is what the distribution assumption refers to) is possibly a beta distribution. – BigBendRegion Aug 16 '21 at 18:24
  • The distribution is left-skewed, not right-skewed. – Nick Cox Aug 16 '21 at 21:03
  • Left skewness introduces no special problems. The answer to the general question in the title is "run the GLM on the negative of the response variable, then negate all the coefficient estimates." This is why most distributional families that have been studied concern distributions with zero or positive skewness: they still cover all the possibilities. – whuber Aug 18 '21 at 12:18

1 Answers1

2

As commented by @Dave and as probably pointed out many times on CV (e.g. here and here), you shouldn't worry about the marginal ("overall") distribution of the response, but the conditional distribution (which you have, by looking at the histogram of the residuals).

Depending on what you're doing, you might not even need to worry about the non-Normality in the residuals/conditional distribution. Linear models (including LMM) are pretty robust to moderate amounts of non-Normality. That said, if you are modeling responses on a 0-1 scale, you might want to worry about issues like nonlinearity, ceiling effects (i.e. what happens when relative recall gets close to a boundary at 1?), and heteroscedasticity, all of which are potentially bigger issues than the mere lack of Normality in the residuals.

If relative recall is measured on a continuous (0,1) scale, and if there are no exact 0/1 values, it probably makes most sense to model it as a Beta distribution. (Also assuming that this is not a ratio with a known denominator, e.g. 5/17, in which case it's probably best to use a binomial model). There are several R packages that can fit mixed-effect beta models (glmmTMB, brms, mgcv, INLA, gamlss).

For example, if the number of items offered to each subject in each category (i.e. the number of items making up the denominator of each computed relativerecall observation) is stored as N in the data set, then the model fit

model <- FUN(relativerecall ~ A*B + (1|subject), 
           data = df, 
           weights = N,
           family=binomial)

where FUN is either lme4::glmer or glmmTMB::glmmTMB, should work and should give nearly identical results. The weights argument is important ...

If you have a significant number of exact-0 or exact-1 values (so many that "squeezing" slightly to get them off the boundary seems dicey) you'll need a zero-inflated or zero-one-inflated Beta mixed model, which limits your choices slightly further.

Ben Bolker
  • 34,308
  • 2
  • 93
  • 126
  • Thanks, Ben. My data is a ratio however the denominator changes by each calculated observation. I do not have any exact 0 values (lowest is 0.07), however I do have exact 1 values. In which case, which approach do you suggest I continue with? Thank you very much. – aperis Aug 17 '21 at 14:04
  • are the denominators known, and integers? if so then binomial (or *possibly* quasibinomial/beta-binomial) are definitely your best bet – Ben Bolker Aug 17 '21 at 14:22
  • The denominator is known but it is different for each observation. The denominators are integers as they are the total amount of remembered items amongst a list. I don't understand how my data follow a binomial distribution. I now ran: model – aperis Aug 17 '21 at 17:07
  • see edits. If you're going to use type-3 Anova you had better make sure that you're using sum-to-zero contrasts too ... (see documentation in the `car` package) – Ben Bolker Aug 17 '21 at 19:04