2

Im analysing count data (number of clinic visits) when I test for poisson distribution using 1 sample KS test in spss the sig is <0.05( meaning it doesnt follow poisson distribution ) it does not follow normal distribution either, no values of zero, the values are either 1,2,3,or 5, what can I do

maryam
  • 21
  • 2
  • 1
    What are you trying to do? – Peter Flom Nov 26 '15 at 22:35
  • Why do you need that to be Poisson (or normal, or anything else)? – Glen_b Nov 26 '15 at 23:39
  • Im studying several independent variables and their effect on the number of clinical visits( count data), and I read that it is wrong to deal with count data as continuous, we should use regression models for count data . the number of clinical visits is under-dispersed ( value of pearson chi square goodness of fit / df = 0.25) should I go ahead and use poisson or not – maryam Nov 29 '15 at 19:14
  • Has anyone got a basic easy to understand answer for this question? What do you do if you are dealing with count data and do not meet the assumption of the count data following the poisson distribution? Do you use a different type of regression? – Grace Carroll Aug 30 '19 at 14:32

2 Answers2

5

You may be worried about the wrong thing.

For example you were trying to perform a Poisson regression (fit a Poisson GLM), there's no requirement for the marginal distribution of the response to be Poisson. (Similar comments apply with the normal, whether you're using inference via regression or t-tests)

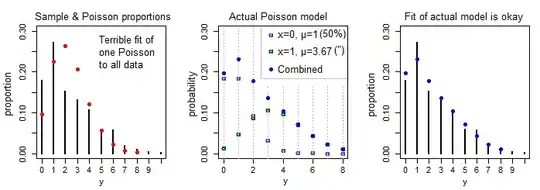
Here's an example where we're fitting a Poisson to $y$ which has different mean when $x=0$ and $x=1$:

enter image description here

(We don't really care about the fit to the margin, what matters is the suitability of the conditional distribution at x=0 and x=1; if both of those are adequate descriptions -- i.e. does the purple describe what happens when x=0 and the green when x=1 -- the marginal distribution will take care of itself.)

Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • I have red your answer three times but still I cannot realize that. What do you mean by marginal distribution, $pr(Y|X=x)$ ? – TPArrow Nov 27 '15 at 17:09
  • $\text{pr}(Y|X=x)$ is the conditional distribution (a different one for each $x$). The marginal distribution is just $\text{pr}(Y)$, which is an aggregate (more specifically a weighted average) over the individual conditional distributions. – Glen_b Nov 28 '15 at 00:00
-1

Try zero truncated poisson or zero truncated negative binomial regression

Zico
  • 19
  • 4