Suppose that we have a random variable $X$ and this is a function of an index $t\in T$.
Here, what is the meaning of the infimum of this random function? $$\inf_{t\in T}X(t)$$
How can we interpret that quantity, despite the fact that for a given $t$, $X(t)$ is a random variable?
Because you're getting some misleading comments, I will offer a more detailed answer. The idea is that when you observe a "random function," you have in hand a "realization" of it. This realization is an ordinary (completely determined) function. You are just computing its infimum in the usual sense (as I will explain).
Before we move on, let's avert a potential misconception. Notice this description has nothing to do with the probability law governing the random function. Abstractly, a random (real-valued) function defined on a set $T$ is a map $X: \Omega\to \mathbb{R}^T$ where $\mathbb{R}^T$ is the set of all functions from $T$ to $\mathbb R$ and $\Omega$ is a probability space. The infimum can be considered a map from $\mathbb{R}^T$ into $\mathbb R.$ Composing the infimum with $X$ yields a function from $\Omega$ to $\mathbb R:$ that is, a random variable.
I am purposely not mentioning the technical detail of measurability because that's not an essential part of the idea; but even for those familiar with the details, you will observe they depend only on various sigma algebras that one must define, but they still don't depend on any particular probability distribution.
When you consider a collection of random variables $X_t$ as a "random function" of a domain $T,$ this collection is known as a stochastic process.
The description I gave of this concept at General Definition of Stochastic Processes invites you to think of a "box" of possible realizations $x_t$ of $X_t:$ each of these realizations can be represented as the graph of $x_t$ versus $t$ written on a slip of paper (a "ticket"). Think of $X_t$ as arising by selecting one of these tickets randomly.
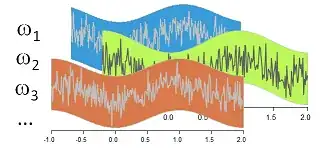
This figure from the referenced post displays three such tickets, named $\omega_1,\omega_2,$ and $\omega_3.$ Evidently $T=[-1,2]$ is an interval of real numbers in this example.
The graph of a (non-random, ordinary) function $x$ is, by definition, the set of all ordered pairs $(t,x_t).$ Ignoring the index $t$ leaves us a set of all values $\{x_t\mid t\in T\}$ (the image of $x$). When these values are real numbers, the Completeness axiom of real numbers asserts they have a unique greatest lower bound, or infimum. (It is convenient to declare that the infimum of a set with no lower bound nevertheless exists and to call it "$-\infty.$")
Here, then, is a way to think of the infimum of a random function aka stochastic process:
On each ticket $x$ in the box for the process $X$, write down the infimum of its values; namely, the number $\inf_{\,t\in T}x_t.$ Drawing a ticket randomly from this box, and reading only this number, models the meaning of $\inf_{\,t\in T}X_t:$ it is a random variable.
Any textbook covering stochastic processes will assume you are familiar with the analysis of functions. That includes most concepts from Calculus and elementary Analysis. I imagine many of those texts will freely use notation like the one we're using here for infima to extend any property of functions to corresponding properties of random functions in exactly the same way.
