glmer gamma model - good fit?

Question

I am running a glmer model

    glmer(RT ~ Prob * Bl * Session * Gr + (1  | Participant), 
          data= Data.trimmed, family = Gamma(link = "log"), 
            control=glmerControl(optimizer="bobyqa", 
            optCtrl=list(maxfun=1000000)), nAGQ = 0)

with gamma family and I am trying to determine whether this model shows a good fit. It doesn't seem like it does, but I would like to get someone else's opinion since these models are a lot more complicated to deal with. If you think this is poorly fit, do you have any suggestion for how to improve the model?
I have 209062 rows of data and this is response time data. I want to determine whether there differences between groups (Gr - 2 levels) on the learning of a task (Pr - 2 levels) across time (within sessions - Bl - 4 levels / across sessions - Session - 2 levels). It doesn't have zero response times, but some close to zero. I have also added the lmer model at the end.

Glmer Model summary:

Generalized linear mixed model fit by maximum likelihood (Adaptive Gauss-Hermite Quadrature, nAGQ = 0) ['glmerMod']
 Family: Gamma  ( log )
Formula: RT ~ Probability * Block * Session * Group + (1 | Participant)
   Data: Data.trimmed
Control: glmerControl(optimizer = "bobyqa", optCtrl = list(maxfun = 1e+06))

     AIC      BIC   logLik deviance df.resid 
 2456107  2456538 -1228012  2456023   209020 

Scaled residuals: 
   Min     1Q Median     3Q    Max 
-4.297 -0.625 -0.158  0.440 35.691 

Random effects:
 Groups      Name        Variance Std.Dev.
 Participant (Intercept) 0.002203 0.04694 
 Residual                0.053481 0.23126 
Number of obs: 209062, groups:  Participant, 130

Fixed effects:
                                        Estimate Std. Error  t value Pr(>|z|)    
(Intercept)                            6.024e+00  4.182e-03 1440.439  < 2e-16 ***
Probability1                          -2.835e-02  7.041e-04  -40.265  < 2e-16 ***
Block2-1                              -2.925e-02  2.077e-03  -14.084  < 2e-16 ***
Block3-2                              -3.676e-03  2.131e-03   -1.725 0.084500 .  
Block4-3                               4.085e-03  2.307e-03    1.771 0.076577 .  
Block5-4                              -1.220e-02  2.380e-03   -5.125 2.98e-07 ***
Session1                               4.795e-02  7.323e-04   65.478  < 2e-16 ***
Group1                                -4.616e-02  4.182e-03  -11.037  < 2e-16 ***
Probability1:Block2-1                 -7.228e-03  2.077e-03   -3.480 0.000501 ***
Probability1:Block3-2                 -5.332e-03  2.131e-03   -2.503 0.012331 *  
Probability1:Block4-3                 -2.076e-02  2.307e-03   -8.999  < 2e-16 ***
Probability1:Block5-4                  6.044e-03  2.380e-03    2.539 0.011104 *  
Probability1:Session1                  1.656e-03  7.046e-04    2.351 0.018743 *  
Block2-1:Session1                     -1.972e-02  2.077e-03   -9.494  < 2e-16 ***
Block3-2:Session1                     -8.521e-03  2.131e-03   -3.999 6.35e-05 ***
Block4-3:Session1                      4.380e-05  2.308e-03    0.019 0.984856    
Block5-4:Session1                     -3.768e-03  2.380e-03   -1.583 0.113389    
Probability1:Group1                    1.515e-03  7.041e-04    2.151 0.031478 *  
Block2-1:Group1                       -6.161e-03  2.077e-03   -2.966 0.003015 ** 
Block3-2:Group1                       -1.129e-02  2.131e-03   -5.301 1.15e-07 ***
Block4-3:Group1                        7.095e-03  2.307e-03    3.076 0.002101 ** 
Block5-4:Group1                       -4.055e-03  2.380e-03   -1.704 0.088414 .  
Session1:Group1                        3.782e-03  7.323e-04    5.164 2.41e-07 ***
Probability1:Block2-1:Session1         5.729e-05  2.077e-03    0.028 0.977997    
Probability1:Block3-2:Session1         3.543e-03  2.131e-03    1.663 0.096363 .  
Probability1:Block4-3:Session1        -6.877e-03  2.308e-03   -2.980 0.002886 ** 
Probability1:Block5-4:Session1         4.329e-03  2.380e-03    1.819 0.068952 .  
Probability1:Block2-1:Group1          -1.238e-03  2.077e-03   -0.596 0.550980    
Probability1:Block3-2:Group1           1.022e-02  2.131e-03    4.795 1.63e-06 ***
Probability1:Block4-3:Group1          -6.532e-03  2.307e-03   -2.831 0.004634 ** 
Probability1:Block5-4:Group1           2.351e-03  2.380e-03    0.988 0.323373    
Probability1:Session1:Group1          -1.805e-03  7.046e-04   -2.562 0.010412 *  
Block2-1:Session1:Group1              -2.060e-04  2.077e-03   -0.099 0.920984    
Block3-2:Session1:Group1              -4.211e-03  2.131e-03   -1.977 0.048094 *  
Block4-3:Session1:Group1               3.339e-03  2.308e-03    1.447 0.147888    
Block5-4:Session1:Group1              -3.956e-03  2.380e-03   -1.662 0.096539 .  
Probability1:Block2-1:Session1:Group1 -1.270e-03  2.077e-03   -0.611 0.540933    
Probability1:Block3-2:Session1:Group1  1.678e-03  2.131e-03    0.788 0.430929    
Probability1:Block4-3:Session1:Group1 -4.640e-03  2.308e-03   -2.010 0.044392 *  
Probability1:Block5-4:Session1:Group1  4.714e-03  2.380e-03    1.980 0.047649 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation matrix not shown by default, as p = 40 > 12.
Use print(x, correlation=TRUE)  or
    vcov(x)        if you need it

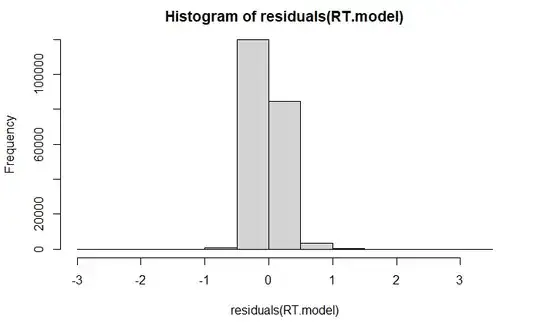
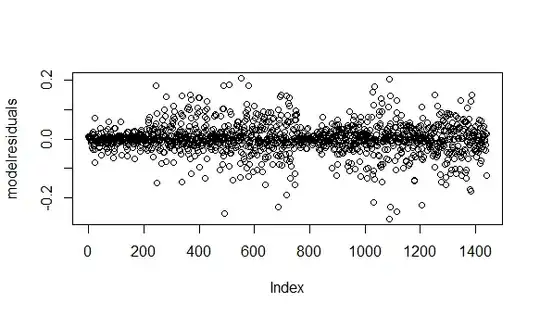
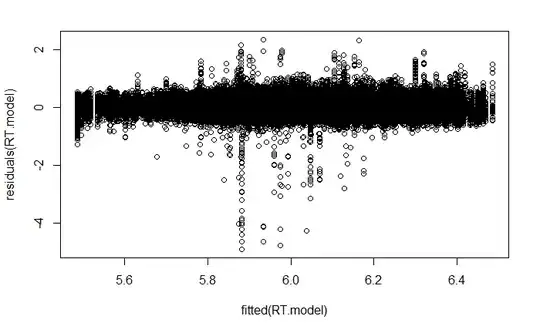
plotting residuals:

qqplot

plot(fitted(RT.model), residuals(RT.model))

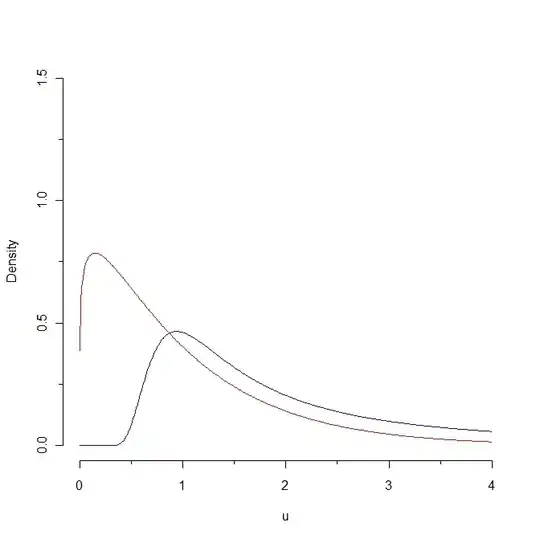
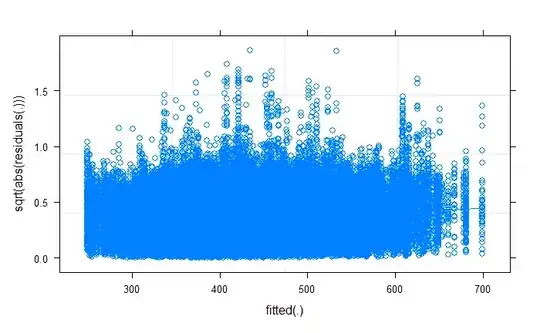
Dharma plot:

plot(RT.model,sqrt(abs(residuals(.))) ~  fitted(.), 
            type=c("p","smooth"))

For the lmer model:

RT.model <- lmer(logRT ~ Probability * Block * Session * Group + (1  | Participant), data= Data.trimmed)


Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
Formula: logRT ~ Probability * Block * Session * Group + (1 | Participant)
   Data: Data.trimmed

REML criterion at convergence: -51844.2

Scaled residuals: 
     Min       1Q   Median       3Q      Max 
-23.0325  -0.6283  -0.0801   0.5553  11.0990 

Random effects:
 Groups      Name        Variance Std.Dev.
 Participant (Intercept) 0.02413  0.1553  
 Residual                0.04541  0.2131  
Number of obs: 209062, groups:  Participant, 130

Fixed effects:
                                        Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)                            5.999e+00  1.364e-02  1.283e+02 439.726  < 2e-16 ***
Probability1                          -2.731e-02  6.488e-04  2.089e+05 -42.087  < 2e-16 ***
Block2-1                              -2.597e-02  1.914e-03  2.089e+05 -13.569  < 2e-16 ***
Block3-2                              -6.639e-03  1.963e-03  2.089e+05  -3.381 0.000721 ***
Block4-3                               3.532e-03  2.126e-03  2.089e+05   1.662 0.096610 .  
Block5-4                              -1.598e-02  2.193e-03  2.089e+05  -7.287 3.18e-13 ***
Session1                               4.636e-02  6.754e-04  2.090e+05  68.638  < 2e-16 ***
Group1                                -4.793e-02  1.364e-02  1.283e+02  -3.513 0.000613 ***
Probability1:Block2-1                 -7.919e-03  1.914e-03  2.089e+05  -4.138 3.51e-05 ***
Probability1:Block3-2                 -3.684e-03  1.963e-03  2.089e+05  -1.877 0.060567 .  
Probability1:Block4-3                 -2.211e-02  2.126e-03  2.089e+05 -10.399  < 2e-16 ***
Probability1:Block5-4                  6.860e-03  2.193e-03  2.089e+05   3.128 0.001763 ** 
Probability1:Session1                  2.198e-03  6.493e-04  2.089e+05   3.385 0.000711 ***
Block2-1:Session1                     -1.879e-02  1.914e-03  2.089e+05  -9.817  < 2e-16 ***
Block3-2:Session1                     -7.896e-03  1.963e-03  2.089e+05  -4.022 5.78e-05 ***
Block4-3:Session1                     -1.407e-03  2.126e-03  2.089e+05  -0.661 0.508296    
Block5-4:Session1                     -5.281e-03  2.193e-03  2.089e+05  -2.408 0.016046 *  
Probability1:Group1                    1.695e-03  6.488e-04  2.089e+05   2.612 0.009010 ** 
Block2-1:Group1                       -7.155e-03  1.914e-03  2.089e+05  -3.739 0.000185 ***
Block3-2:Group1                       -1.071e-02  1.963e-03  2.089e+05  -5.453 4.96e-08 ***
Block4-3:Group1                        6.027e-03  2.126e-03  2.089e+05   2.835 0.004578 ** 
Block5-4:Group1                       -1.975e-03  2.193e-03  2.089e+05  -0.900 0.367938    
Session1:Group1                        3.271e-03  6.754e-04  2.090e+05   4.843 1.28e-06 ***
Probability1:Block2-1:Session1         3.932e-05  1.914e-03  2.089e+05   0.021 0.983609    
Probability1:Block3-2:Session1         2.946e-03  1.963e-03  2.089e+05   1.500 0.133491    
Probability1:Block4-3:Session1        -5.279e-03  2.127e-03  2.089e+05  -2.482 0.013068 *  
Probability1:Block5-4:Session1         4.600e-03  2.193e-03  2.089e+05   2.098 0.035950 *  
Probability1:Block2-1:Group1          -1.013e-03  1.914e-03  2.089e+05  -0.529 0.596705    
Probability1:Block3-2:Group1           1.014e-02  1.963e-03  2.089e+05   5.165 2.41e-07 ***
Probability1:Block4-3:Group1          -6.676e-03  2.126e-03  2.089e+05  -3.140 0.001687 ** 
Probability1:Block5-4:Group1           2.475e-03  2.193e-03  2.089e+05   1.129 0.259079    
Probability1:Session1:Group1          -1.077e-03  6.493e-04  2.089e+05  -1.658 0.097259 .  
Block2-1:Session1:Group1               2.446e-03  1.914e-03  2.089e+05   1.278 0.201365    
Block3-2:Session1:Group1              -3.793e-03  1.963e-03  2.089e+05  -1.932 0.053342 .  
Block4-3:Session1:Group1               1.633e-03  2.126e-03  2.089e+05   0.768 0.442515    
Block5-4:Session1:Group1              -2.495e-03  2.193e-03  2.089e+05  -1.137 0.255393    
Probability1:Block2-1:Session1:Group1 -2.243e-03  1.914e-03  2.089e+05  -1.172 0.241206    
Probability1:Block3-2:Session1:Group1  1.190e-03  1.963e-03  2.089e+05   0.606 0.544432    
Probability1:Block4-3:Session1:Group1 -3.378e-03  2.127e-03  2.089e+05  -1.588 0.112179    
Probability1:Block5-4:Session1:Group1  5.139e-03  2.193e-03  2.089e+05   2.343 0.019126 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation matrix not shown by default, as p = 40 > 12.
Use print(x, correlation=TRUE)  or
    vcov(x)        if you need it

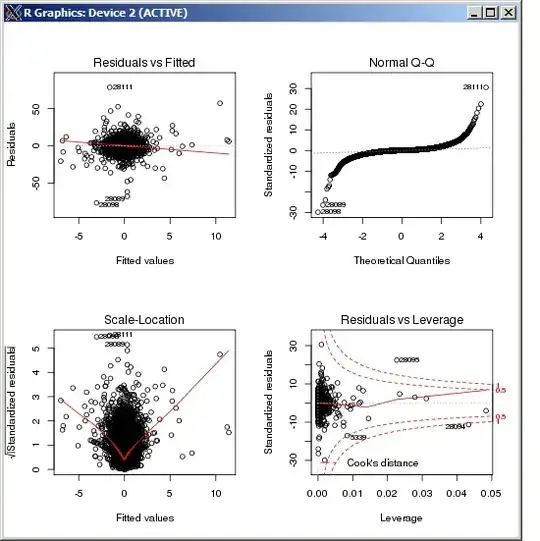
plotting residuals

plot(fitted(RT.model),residuals(RT.model))

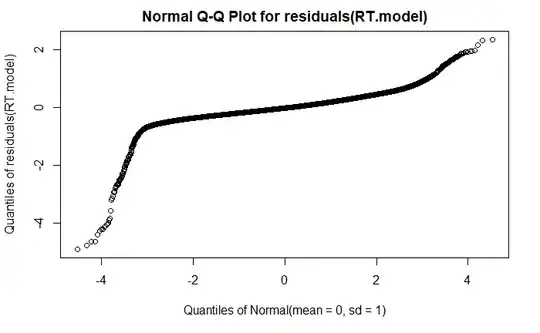
qqplot

DHARMa plot

There are many similar posts, like https://stats.stackexchange.com/questions/390063/what-are-the-assumptions-of-a-gamma-glm-or-glmm-for-hypothesis-testing some comments: 1) The histogram has way to few points to be useful! 2) There are no normal assumption in a gamma glm, so why a normal qqplot? Try simulated residuals, see example at https://stats.stackexchange.com/questions/295340/what-to-do-with-glm-gamma-when-residuals-are-not-normally-distributed/302413#302413 3) In the other plots, there is way to much overplotting. Use smaller symbols and transparency — kjetil b halvorsen, Jul 12 '21 at 22:07
I used the DHARMa plots as you can see and they look disappointing. I did fit a nlme model as well which gave the exact same results but this model's fit seems very poor. — CatM, Jul 12 '21 at 23:02
I agree, but without more onformation on data and model, variables used we can say no more! — kjetil b halvorsen, Jul 12 '21 at 23:08
all variables are categorical and dependent variable is response times, I'm going to add this to the post — CatM, Jul 12 '21 at 23:09
What is the goal of modeling? Prediction, interpretation? There is way to many extreme residuals for a gamma model, is there many zero response times? Please tell us a lot of the context — kjetil b halvorsen, Jul 12 '21 at 23:18
I want to determine whether there differences between groups (Gr - 2 levels) on the learning of a task (Pr - 2 levels) across time (within sessions - Bl - 4 levels / across sessions - Session - 2 levels). It doesn't have zero response times, but some close to zero. — CatM, Jul 12 '21 at 23:21
Your response variable is `logRT`, is it already logged? For a gamma glm it should not be! Otherwise, there is not enough information in your Q for me to say more, Maybe include better information & better plots, or even share the data? Or maybe ask a new question about alternatives to gamma glm's when the gamma model dont have capacity to fit the variance (or outliers)? — kjetil b halvorsen, Jul 13 '21 at 15:25
Yes, I do have logRT but the plots look very much identical with RT as DV or logRT. Yet, the model fails to converge when using RT. Which plots would you recommend using? Just changed all plots to show the results for "RT" instead of logRT. — CatM, Jul 13 '21 at 17:18
At least I would give the summary of the model fit, and do what I said above about more bins, smaller symbols and transparency ... — kjetil b halvorsen, Jul 13 '21 at 17:32
I am sorry, I should have added the output. It never crossed my mind. I added a better plot for the residuals (I think). I think the problem is the left side, there are a lot more data points than there should be for a gamma distribution. I under if the best option would be truncate the data but not sure if removing data points means losing important information, since one of the groups is clearly faster than the other and there's theoretical reasons for why this happens. — CatM, Jul 13 '21 at 18:11
One option is to try ordinal regression, see for instance https://stats.stackexchange.com/questions/410421/analysis-for-ordinal-categorical-outcome — kjetil b halvorsen, Jul 13 '21 at 18:19
Throwing in a quick two cents after reading through this, have you tried an ex-gaussian regression? I don't have much personal experience with modeling reaction time data, but I see these models commonly run where the assumption is an ex-gaussian distribution. Also possible that you need to run a distributional model where there are other variables predicting the gamma's shape value. Gamma assumes variance increases with the mean, but running a distributional model lets you also add other predictors of that shape distribution parameter — Billy, Jul 13 '21 at 18:55
What do the distributions of residuals look like if you subdivide them by predictor category? — Ben Bolker, Jul 13 '21 at 23:38
@BenBolker Bolker which predictor? Should I do that for all? — CatM, Jul 14 '21 at 00:51
I was thinking that you could draw Q-Q plots for all of the predictor combinations (I guess there are 40?) Since you've fit a "saturated" model (all possible interactions of categorical predictors), there can't be any problems with linearity (mean values). — Ben Bolker, Jul 14 '21 at 01:32
I am sorry for bothering you again but is there any efficient way of doing the qq plots for each combination? — CatM, Jul 14 '21 at 02:01

glmer gamma model - good fit?

0 Answers0