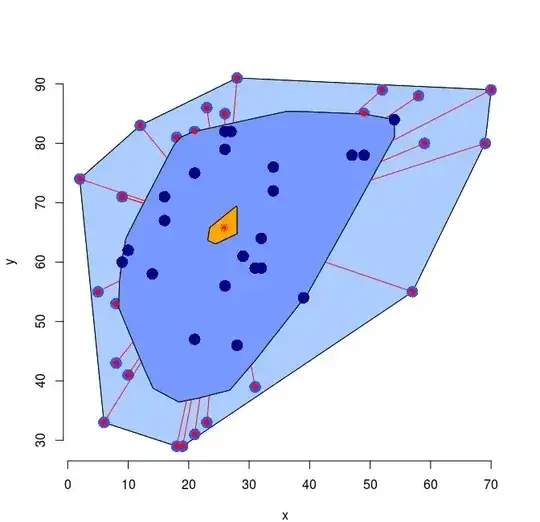
I have been given a set of data points $(x_i,y_i)$. I have to plot a scatter plot and determine if there are any outliers. But I haven't been taught a method to measure which data point is an outlier and which is not. So how can I do it for example in Sage or R? I found by Google that there is at least two tests to do that, Dixon's and Grubbs's test, so which one should I learn in this problem?
x = c(1,34,6,47,10,49,23,32,12,16,29,49,28,8,57,9,31,10,21,26,31,52,21,8,18,5,18,
26,27,26,32,2,59,58,19,14,16,9,23,28,34,70,69,54,39,9,21,54,26)
y = c(47,76,33,78,62,78,33,64,83,67,61,85,46,53,55,71,59,41,82,56,39,89,31,43,29,55,
81,82,82,85,59,74,80,88,29,58,71,60,86,91,72,89,80,84,54,71,75,84,79)