As an approximation, assume all observations within an interval
are located at its center.
Then you have four midpoints $m_j$ with corresponding frequencies $f_j$
for $j = 1,2,3,4.$ where $n = \sum_j f_n = 814.$ Then $\bar X \approx \frac 1n\sum_j f_jm_j = 53.51,$ and $S = \sqrt{S^2} = 21.84,$ in thousands of dollars, where $S^2 \approx \frac{1}{n-1}\sum f_j(m_j-\bar X)^2.$ [Using R.]
m = c(15, 30, 60, 90)
f = c(44, 240, 400, 130)
[1] 814
a = sum(f*m)/n; a
[1] 53.51351
s = sqrt(sum(f*(m-a)^2)/(n-1)); s
[1] 21.84175
A more elaborate and perhaps slightly more accurate method is to
'reconstruct' the sample by assuming that observations are spread
uniformly at random in their respective intervals. Notice that this is
a random reconstruction and additional runs of the 'reconstruction' program
(without using the set.seed statement) will give slightly different
answers.
set.seed(623)
x = c(runif(44, 10, 20), runif(240, 20, 40),
runif(400,40, 80), runif(130, 80,100))
mean(x); sd(x)
[1] 53.84582
[1] 23.48832
The approximate mean $\bar X \approx 53.8$ and standard deviation $S\approx 23.5$
are not much different from the previous approximations.
A histogram based on the given intervals roughly suggests the
shape of the sample from which such a sample might have been taken.
It seems unlikely that the distribution of if incomes is normal. [Tick marks. from rug,
along the horizontal axis show the locations of the reconstructed data values.]
hist(x, br=c(10,20,40,80,100)); rug(x)
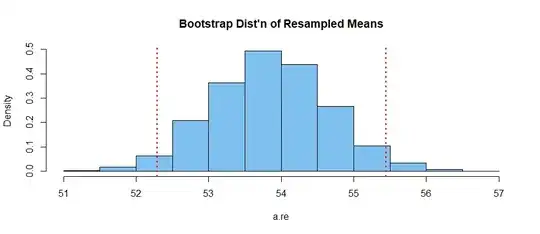
Using the reconstructed the sample,
one can get one kind of 95% bootstrap confidence interval $(52.3,\, 55.4)$, in which
the population mean $\mu$ might lie.
set.seed(2021)
a.re = replicate( 4000, mean(sample(x,rep=T)) )
ci = quantile(a.re, c(.025,.975)); ci
2.5% 97.5%
52.28877 55.44453
hist(a.re, prob=T)
hdr = "Bootstrap Dist'n of Resampled Means"
hist(a.re, prob=T, col="skyblue2", main=hdr)
abline(v=ci, col="red", lwd=2, lty="dotted")
Note: As @NickCox has suggested, alternate methods of approximation
and reconstruction might be used if you have some idea of the shape of
the income distribution. Also, as here, using beta distributions to reconstruct the lowest and highest intervals might be more realistic.

