1

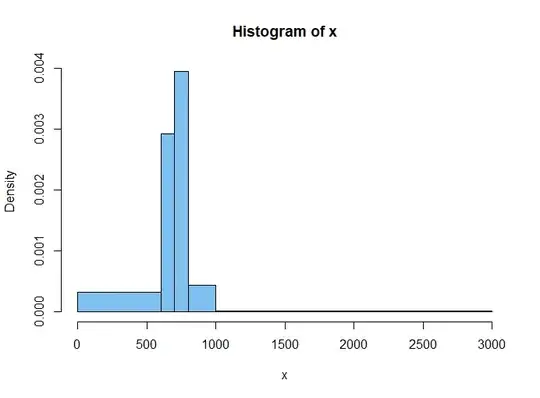
I have a set of data in histogram format with uneven bin sizes, which represents the weight of horses at a certain point in their lifetimes when they are switched from grazing to a racing diet.

$Weight - Headcount\\ 0-600lb: 340,000\\ 600-699lb: 365,000\\ 700-799lb: 494,000\\ 800-899lb: 430,000\\ 900-999lb: 110000\\ 1000-3000lb: 40,000$

I need some kind of estimation of the number of horses which weigh $x\;lb$. My initial thought would be to fit some kind of curve/distribution (lognormal?), but I'd gladly take any suggestions! I can't really fit to the midpoints of each bin, since the first and last bins are fairly highly weighted towards the upper and lower ends of the bands respectively.

It may also be possible that this is a combination of two distributions - male and female horses, which overlap around their means.

John Horserider
  • 13
  • 3
  • Do you know anything about the distributions within the bins? – Dave Jun 18 '21 at 16:18
  • Only that it should be uniformly decreasing towards the tails. 1000-3000 should pretty much be 0 at around 1400lb. – John Horserider Jun 18 '21 at 16:47
  • [Re;ated Q &A](https://stats.stackexchange.com/questions/531794/how-to-calculate-the-mean-from-bin-endpoints-and-frequencies/531822#531822) – BruceET Jun 23 '21 at 08:17

1 Answers1

1

Maybe something like this. Beta distributions for the first and last intervals put few points towards the extremes. Otherwise, observations are spread randomly within their intervals.

 x = c(600*rbeta(340000, 3,1), 
      runif(365000, 600,700),
      runif(494000, 700,800),
      runif(110000, 800,1000),
      1000 + 2000*rbeta(40000, 1,3))

cutp= c(0,600,700,800,1000,3000)  # interval boudaries
hist(x, br=cutp, col="skyblue2")

enter image description here

    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
  5.554  578.595  684.654  673.490  759.426 2947.059 
[1] 1399000  # sample size
[1] 220.179  # sample SD

A more sensible histogram (with equal bin widths):

hist(x, col="skyblue2")

enter image description here

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • A beta distribution does look pretty good on the tail ends - but for everything else it seems to me that there is a clearly defined maxima and the curve is decreasing from thereon out rather than randomly distributed. I was thinking of fitting a distribution to the curve, but the problem with that is I know the buckets are absolutely right and the fit won't be perfect, so I need some way to adjust the point estimates for each weight bracket so they add up to each bracket (since under/overestimating by several horses is worse than a few lb). – John Horserider Jun 22 '21 at 08:20
  • You may be overthinking this. You correctly mentioned in your Question that the main difficulty is in the first and last bins. If you knew enough to fuss usefully with the rest, you would essentially know the shape of the distribution (including mean and SD) without having to make a histogram. // A problem with binning data is that useful information may be lost beyond hope of retrieval; using many bins of equal widths sometimes helps retain information--even if that leads to an ugly histogram. – BruceET Jun 22 '21 at 08:55