T-test states difference of donation is significant when Z-test claims not, what method to use?

Question

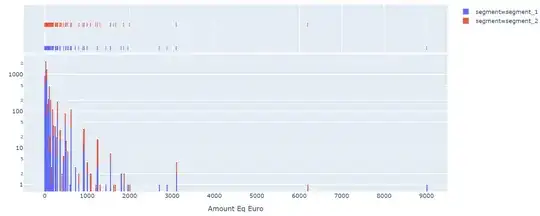
I have two populations who have been exposed to two different websites that should bring them to donations: one with a progress bar that pushes them to give (B, segment 2) and the other not (A, segment 1).

And with log(y):

I have noticed that, on average, population B gives much more than A:

                 s1          s2
count   3352.000000 3053.000000
mean    86.137828   109.417294
std     239.235495  231.897494
min     2.000000    3.000000
25%     20.000000   25.000000
50%     30.000000   50.000000
75%     60.000000   100.000000
max     9000.000000 6200.000000

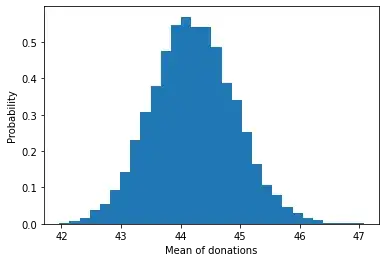
But the mean of sampled donations looks normal:

means = []
for i in range(0,10000):
  means.append(df["Amount Eq Euro"].sample(8007, replace=True).mean())

import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline

np.random.seed(42)

plt.hist(means, density=True, bins=30)  # density=False would make counts
plt.ylabel('Probability')
plt.xlabel('Mean of sample donations');

So I wanted to know what method should I use to test that. Should I use a t-test or an z-test? Because a colleague chose the t-test and found out that the difference was significant but I chose z-test and didn't.

Z-test

Indeed as we’re interested in the average donation, this averaging of an underlying distribution meant to mean that our final estimate cound well be approximated by a normal distribution. Which could look like this:

df_segment_2 = df[df.Campaign.str.contains('segment 2')]['Amount Eq Euro']
df_segment_1 = df[~df.Campaign.str.contains('segment 2')]['Amount Eq Euro']

num_a, num_b = df_segment_1.count(), df_segment_2.count()
mean_a, mean_b = df_segment_1.mean()    , df_segment_2.mean()
std_a, std_b = df_segment_1.std()   , df_segment_2.std()

# The z-score is really all we need if we want a number
z_score = (mean_b - mean_a) / np.sqrt(std_a**2 + std_b**2)
print(f"z-score is {z_score:0.3f}, with p-value {norm().sf(z_score):0.3f}")

But when doing the difference between the two curves I find that the z-score is 0.070, with p-value 0.472. So it's not significant.

I know that the difference from the Z Test is that we do not have the information on Population Variance here. We use the sample standard deviation instead of population standard deviation in this case. But in my case, I can get the standard deviation from my data, isn't it? Or should I need to do a population standard deviation and use t-test?

I even simulated with:

n = 10000
means_a = norm(mean_a, std_a).rvs(n)
means_b = norm(mean_b, std_b).rvs(n)
b_better = (means_b > means_a).mean()
print(f"B is better than A {b_better:0.1%} of the time")

And found out that B is better than A only 53.0% of the time.

T-test

I even tried with t-test

import scipy.stats as stats

stats.ttest_ind(a=df_segment_1, b=df_segment_2, equal_var=True)

Which returns:

Ttest_indResult(statistic=-3.946818060072667, pvalue=8.004451431980152e-05)

So it rejects the hypothesis as p_val is 8.004451431980152e-05 so it is significant.

I don't understand why, I don't understand what this test stands for. I thought it was just convenient when we had less than 30 people in a given population

Extra information for @Dave

Here are the statistics for the whole population

count    6405.000000
mean       97.234192
std       236.034497
min         2.000000
25%        20.000000
50%        40.000000
75%        80.000000
max      9000.000000
Name: Amount Eq Euro, dtype: float64

Answer 1

You should not be using t-tests or z-tests because your histograms clearly show that your data is not even remotely normally-distributed. Slight violations of normality are alright, but your data appears to have left-truncation and right-skewness. The tailedness of your distribution might even prevent meaningful estimation of certain parameters. Watch Risk and Fat Tails for an introduction to how properties of tails become problematic for unbiased estimation.

A/B testing is not a specific hypothesis test. It is a term for a randomized experimental design with two groups, and thus is compatible with multiple statistical procedures and tests.

The good news is that you seem to have a decent sample size compared to the number of variables, which allows you to look into models that may require more degrees of freedom. A larger sample size also improves statistical power.

However, you seem to be looking for a simple test that one variable was (stochastically) larger than another. In which case, I recommend you read into the Mann-Whitney U test which has an implementation available in SciPy (since you're a Python coder).

Answer 2

You do not know the population variance. You calculated the sample variance and expect that value to be close to the population variance, but you do not know $\sigma^2$.

Therefore, you may have underestimated the variance. To offset this, we use a test statistic with a heavier tail than the normal distribution. The way the math works out for a test statistic of $\dfrac{\bar{x}-\mu_0}{s/\sqrt{n}}$, the test statistic is distributed as $t_{n-1}$.

As you get a larger and larger $n$, you expect to have a tighter estimate of $\sigma^2$, so if you underestimated the variance, you expect to underestimate by less and less. The tails of the test statistic, therefore, can get lighter. In the limit, as $n\rightarrow\infty$, you know the population variance, and there is a notion of the $t_n$ distribution converging to $N(0,1)$ as $n\rightarrow\infty$. For this reason, one might argue that, for a very large (intentionally vague terminology) $n$, the $z$-test might be a reasonable approximation of the $t$-test. I am not sure that I have seen anyone do this, however, and with any modern data science software having t-test tools built in, I see little reason to do this particular approximation.

This is why your colleague argues that $t$-testing is appropriate here, not $z$-testing.

Answer 3

Comment continued to show Minitab output for pooled 2-sample t test. Maybe you can compare it with your computations.

Two-Sample T-Test and CI 

Sample     N  Mean  StDev  SE Mean
1       3352    86    239      4.1
2       3053   109    232      4.2

Difference = μ (1) - μ (2)
Estimate for difference:  -23.28
95% CI for difference:  (-34.84, -11.72)
T-Test of difference = 0 (vs ≠): 
 T-Value = -3.95  P-Value = 0.000  DF = 6403

Both [test & CI] use Pooled StDev = 235.7018