1

Answer: A probability is an integral of a pmf/pdf. The dexp function does not yield said integral. Thus, the question is wrong at the outset, since the density is not supposed to be zero at a point in a cont. distribution. The probability — the integral — should, which it of course is. $$\int_{{\color{blue}x}}^{{\color{blue}x}} f(x) = 0$$

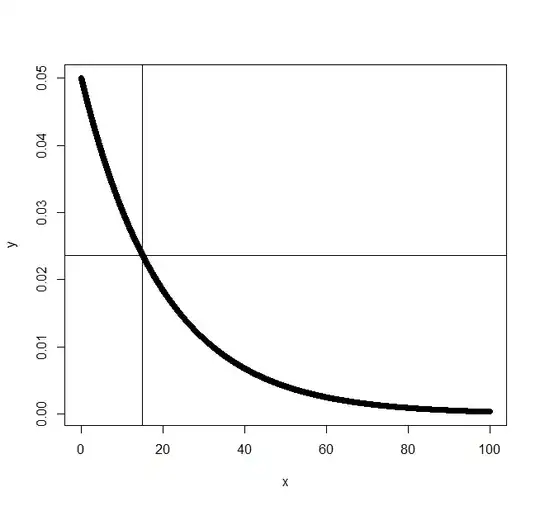
I am working through this video where the "author" states the probability of someone arriving in exactly 15 minutes when one person arrives on average every 20 minutes is 0.

That is, so he explains, because the exponential distribution is continuous. Thus, at any individual point the density is equal to zero.

However, when I enter dexp(15, 1/20) into R I get 0.02361833.

My question is now: Why is R producing this result instead of returning 0?

Or alternatively: Is it wrong that the probability of a single value of a exponential distribution, $P_{exp}(X = x)$, is zero?

Billy
  • 33
  • 3
  • `dexp` is giving you the point on the pdf for x=15. The probability that x=15 is the area under the curve at that single point, which is zero. – Joel Jun 06 '21 at 17:13
  • 1
    I believe that this question is essentially answered here: https://stats.stackexchange.com/questions/4220/can-a-probability-distribution-value-exceeding-1-be-ok – COOLSerdash Jun 06 '21 at 17:55
  • I see. @Joel thank you. – Billy Jun 07 '21 at 12:19

1 Answers1

0

The dexp(x, lambda) call tells you $f_X(x\vert \lambda)$ for $X\sim exp(\lambda)$, that is, the y-axis value for a given x (which can be a vector).

enter image description here

x <- seq(0, 100, 0.01)
y <- dexp(x, 1/20)
plot(x, y)
abline(v = 15)
abline(h = 0.02361833)

The probability of a point in a continuous distribution is zero because $P(X=x) = \int_x^x f_X(u)du$, which you will recognize from calculus as being zero.

Thus, there is no contradiction.

Dave
  • 28,473
  • 4
  • 52
  • 104
  • removed the comment – Billy Jun 07 '21 at 12:15
  • `dexp` is not calculating a probability. Probability is an integral, not a y-axis value. (The y-axis has to do with something called *likelihood*, which has a technical meaning in statistics that is distinct from probability, despite the two words having about the same meaning in colloquial English.) – Dave Jun 07 '21 at 12:17
  • I see. That does make sense. Thank you! – Billy Jun 09 '21 at 11:17