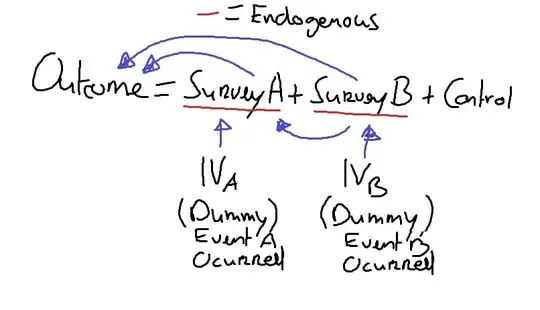
I am estimating a model with two survey questions, which I expect to be endogenous by 2SLS:
$$ Outcome_i = B_0 + B_1SurveyQuestionA_i + B_2SurveyQuestionB_i + B_3Control + u$$
I have an instrumental variable (IV) for $SurveyQuestionA_i$ and an IV for $SurveyQuestionB_i$.
EDIT: The survey questions deal with the perception of the issue related to A and the perception of the issue related to B.
Ben Lambert in this video shows how to do calculate both first stages (although he apparently makes an error when discussing the conditions at the end, see the comments), which is simply including both instruments in both stages;
$$ SurveyQuestionA_i = C_0 + C_1IV_A + C_2IV_B + C_3Controls + v $$ $$ SurveyQuestionB_i = D_0 + D_1IV_A + D_2IV_B + D_3Controls + v $$
In my example, I thought that was kind of odd. Because in my scenario, the IV for $SurveyQuestionA_i$ makes very little sense for $SurveyQuestionB_i$ and vice versa.
Is it not allowed to simply use $IV_A$ for $SurveyQuestionA_i$ and $IV_B$ for $SurveyQuestionB_i$? If not, why not?
NOTE: In case it matters for the question at hand; I am actually utilising a Control Function/ Two Stage Residual Inclusion for the estimation. I did however not want to unnecessarily over-complicate the example.
EDIT: After Adrian's comment I decided to add the output that I have.
First Stages
SurveyQuestionA | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------------------------+----------------------------------------------------------------
IV_B | .1600725 .0270538 5.92 0.000 .1070479 .213097
IV_A | .0009261 .0002869 3.23 0.001 .0003636 .0014885
--------------------------------------------------------------------------------------------
SurveyQuestion_B | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------------------------+----------------------------------------------------------------
IV_B | .4611017 .0273291 16.87 0.000 .4075377 .5146657
IV_A | .0002393 .0002889 0.83 0.407 -.0003268 .0008055
Per Adrian's request, the causal diagram is quite simple (where the arrows are the causal directions). The endogenous variables are correlated.