There are several ways in which you could improve your modeling of these data. Much of what's below is based on what you can learn from Frank Harrell's course notes or book in terms of multiple-regression modeling in general (especially Chapter 4) and Cox survival models in particular (Chapters 20 and 21).
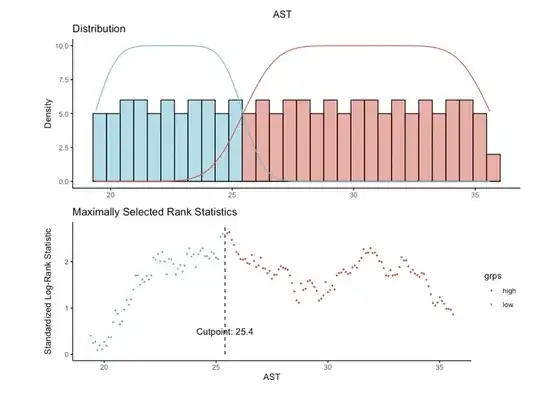
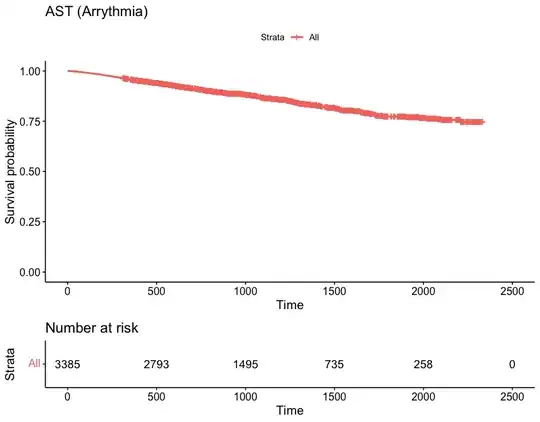
First, do not categorize a continuous predictor based on its association with outcome. See this thread for why categorization is seldom a good idea. Although your p-value of 0.0094 after dichotomizing AST looks very "significant" (graph of survival curves based on the cutoff of 25.4), that p-value is uninterpretable as it doesn't take into account the fact that you used the data to pick the cutoff.*
If you choose a cutoff based on an association with outcome in one particular data set, that "optimal" cutoff will probably not apply to a new data set. Thus your results will not generalize reliably to new data sets, which is typically what one wants to accomplish. You could demonstrate this for yourself: try the automated cutoff choice on multiple bootstrapped samples of your data and see how much the "optimal" cutoffs vary.
Second, a flexible spline model is often the best way to incorporate a continuous predictor into a model when there is no theoretical basis for some fixed functional form. The pspline() function in the R survival package and the rcs() function in the rms package provide different ways to do that.
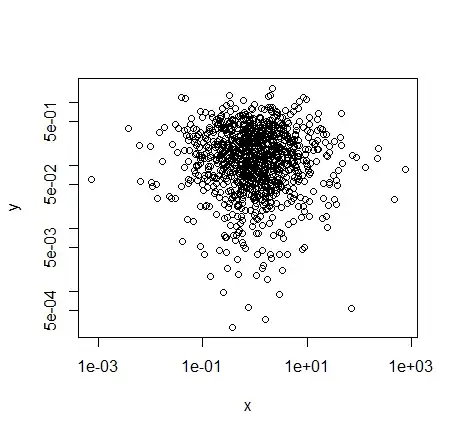
Such modeling lets the data tell you the functional form of how a continuous predictor is associated with outcome. For example, none of the models using AST as a continuous predictor show it to be significantly associated with outcome, but it's treated in those models as linearly associated with log-hazard. If it has a true association with outcome that is more complicated, you could miss it unless you go beyond the linear fit. A spline fit can demonstrate the actual form of its relationship to outcome.
Third, you seem to be starting with a bottom-up approach to modeling, starting with a single predictor of interest (AST) and then adding other predictors (age, sex, BMI). Regression model building better starts with an overview of the data and all the predictors, more of a top-down approach. With survival modeling, look at the number of events as a guide to how complex a model you can build. Then use your knowledge of the subject matter and things like associations among the variables (without considering their associations with outcome in your data) to come up with a set of predictors of a scale consonant with the scale of your data. For survival modeling without overfitting, that's usually about 1 predictor (including interaction terms, extra coefficients for spline fits, etc) per 15 events.
With 425 events in your data set, you might be able to develop a much more complex model. You could use flexible continuous fits not just for AST but also for age and BMI. You could include interactions of those continuous predictors with sex, interactions among the continuous predictors, and additional predictors associated with outcome.
Including as many predictors associated with outcome as possible, without overfitting, is generally a good strategy particularly in survival modeling. In survival modeling, as with logistic regression, omitting any predictor associated with outcome runs a risk of biasing the coefficients of included predictors toward lower than their true magnitudes.
Finally, it's important to document the discrimination and calibration of your model. The concordance index is one measure of discrimination between case outcomes; it's the fraction of pairs of comparable cases in which the model-predicted and observed order of events agrees. (As noted in another answer, that's not very good for your models thus far, as 0.5 is what you get just by chance.) Calibration shows how well things like predicted and observed event probabilities agree over the range of the data. The Harrell reference and the rms package provide tools for evaluating calibration and additional measures of discrimination.
*Given the strong association of age with outcome in the final model, I'm particularly concerned that your 2 AST groups simply differ in average age, so that your AST categories are just a proxy for age.