0

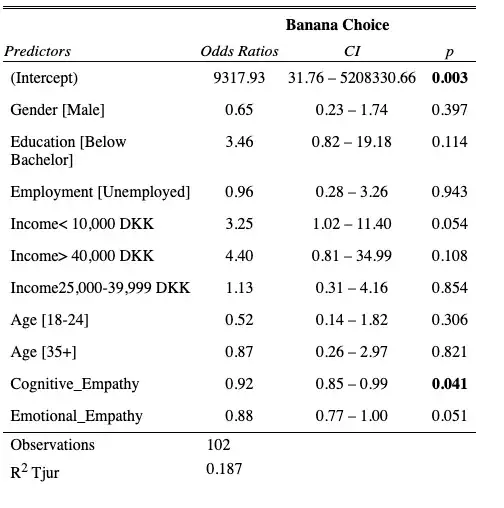
I'm trying to compute multiple logistic regression model and here are the results with covariates and covariates only:

enter image description here

enter image description here

As you can see, I have a very large range of CI and OR. I don't really understand how this happens. Does anyone know how to fix this?

abs(new.data$Cognitive_Empathy)

[1] 54 46 54 58 64 57 49 53 57 62 57 44 60 61 51 64 58 61 58 51 53 62 60 56 54 51 58 53 52 49 53 55 66 52 55 46 54 48
 [39] 58 59 60 57 59 62 46 49 59 63 56 55 55 48 57 53 68 58 49 57 69 62 50 40 59 63 52 60 59 44 53 61 62 59 57 66 60 65
 [77] 57 55 58 67 50 63 60 52 71 51 56 63 52 69 57 56 56 67 48 66 61 46 52 57 53 66

and here are the choices:

[1] Non-organic Non-organic Organic     Non-organic Organic     Organic     Non-organic Non-organic Non-organic
[10] Non-organic Non-organic Organic     Organic     Non-organic Organic     Non-organic Organic     Non-organic
 [19] Non-organic Organic     Organic     Organic     Organic     Organic     Organic     Organic     Organic    
 [28] Organic     Organic     Organic     Organic     Organic     Non-organic Non-organic Organic     Organic    
 [37] Organic     Organic     Non-organic Non-organic Organic     Organic     Organic     Non-organic Organic    
 [46] Non-organic Organic     Non-organic Organic     Organic     Organic     Non-organic Non-organic Organic    
 [55] Non-organic Organic     Organic     Non-organic Organic     Organic     Organic     Organic     Organic    
 [64] Non-organic Organic     Non-organic Non-organic Organic     Organic     Organic     Organic     Organic    
 [73] Non-organic Organic     Non-organic Organic     Organic     Organic     Non-organic Non-organic Non-organic
 [82] Non-organic Organic     Organic     Non-organic Organic     Organic     Non-organic Organic     Organic    
 [91] Non-organic Non-organic Organic     Organic     Organic     Organic     Non-organic Organic     Organic    
[100] Non-organic Organic     Non-organic
Diana Shih
  • 1
  • Only Cognitive Empathy is signif in the top model, and you can see that its 95% CI does not include one. All the other CIs include one and have larger upper bounds, which usually means the association between the predictor variable and outcome are more noisy. Also, look at the s.d. of those variables by themselves - are they greater? Any continuous predictors could also be transformed, in case their scales (range) are widely varying - like caloric consumption per day (e.g. avg=2000) and age. –  Apr 15 '21 at 15:38
  • Assuming the model is a meaningful one (that does not involve irrelevant explanatory variables) and has been correctly specified (that is, its underlying assumptions are good ones), you "fix" it by collecting more data. If you proceed to identify problems in the assumptions and react to them by choosing different variables, expressing the variables differently, selecting subsets of the data, or even choosing different models, then you are *exploring* -- which is fine -- rather than testing; but then the CIs and their p-values become untrustworthy (and usually overly optimistic). – whuber Apr 15 '21 at 17:20

1 Answers1

1

I see two problems here.

First, as @whuber notes in a comment, you probably have insufficient data to fit a model with this many predictors. To avoid overfitting a logistic regression, you should limit yourself to about 1 predictor per 10-20 members of the minority outcome class. With 39 non-organic outcomes, you would be hard pressed to justify more than 4 predictors in a model, while you have about 10 in your first model.

Second, logistic regression has a particular problem when some combination of predictors is completely or nearly completely associated with outcome: (near)-perfect separation. The enormous standard errors for the intercept in the first model suggest that you might be in such a situation, which was alleviated by removing the two predictors to get the second model.

Both of those problems in principle can be worked around with penalized methods like ridge regression that reduce coefficient-magnitude estimates to minimize overfitting.

EdM
  • 57,766
  • 7
  • 66
  • 187