1

Previous reading

Let me first say that I went through this post: (How to determine which distribution fits my data best?) and this post: Assumptions of linear models and what to do if the residuals are not normally distributed, before posting this question. I tried to put everything in subsections to keep the question as clear as possible.

Question:

Can I defend using ols, when my dependent variable is ordinal, if I satisfy all CLM assumptions?

Situation

Sample size: n=23,000

I have a technically ordinal dependent variable (range: 0=no obstacle, 3=severe obstacle) which is distributed as follows:

enter image description here

Because I need the residuals from this regression (explanation why I need the residuals), I would like to NOT treat it as ordinal. This post is essentially about whether I can or not.

My understanding

Now, if I understand correctly, the main reason why I could perhaps not use OLS, would be because the errors/residuals, are not normally distributed:

One of the assumptions of the classical linear model assumptions (CLM), is normality. More specifically, "the population error is independent of the explanatory variables $x_1, x_2, ..., x_k$ and is normally distributed with zero mean and variance $ \sigma: u \sim Normal(0,\sigma^2)$.

So my thought was that, if my residuals are normally distributed, I could defend treating my dependent variable as continuous (please comment).

Alex however additionally mentions the following:

enter image description here

Now, I have to say that my understanding of this requirement is a little bit different (but please correct me if I am wrong). The actual assumption for Multiple Linear Regression, is that the population model is linear in parameters. See also this explanation:

enter image description here

All in all, it appears to me that I can still use OLS to estimate my model.

Nevertheless I am curious, would there be any benefits from choosing for example a quasipoisson model?

What I checked

The first thing I did is to check my residuals:

library(fitdistrplus)
library(logspline)
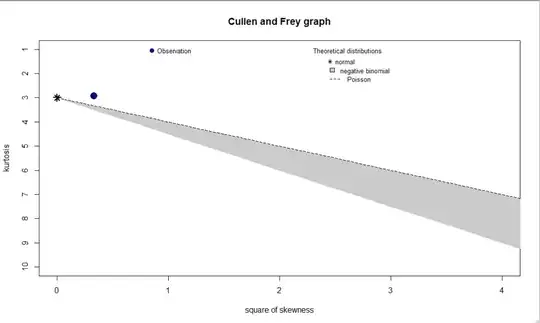
descdist(x, discrete = TRUE)

summary statistics
------
min:  -2.629229   max:  3.123659 
median:  -0.164249 
mean:  -0.000000000000000037898 
estimated sd:  0.9253059 
estimated skewness:  0.5777857 
estimated kurtosis:  2.919639

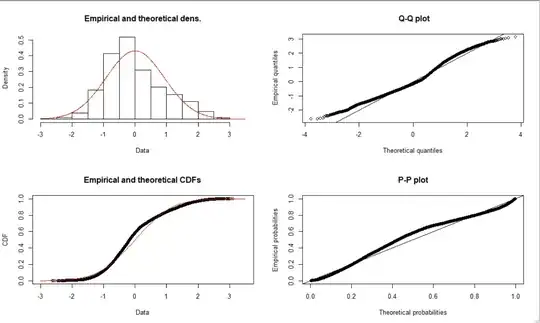
enter image description here

fit <- fitdist(x, "norm")
plot(fit)

enter image description here

Returning to the question

If I am not violating any (CLM) assumptions, can I defend using OLS to estimate my model?

If I can defend this, would there still be anything to gain from using any other model (for example, a quasi poisson) and why then would that be?

Tom
  • 209
  • 4
  • 17
  • 1
    OLS will work for most cases even when the conditional distribution is not Gaussian. It is just that the estimate of the error/variation and associated confidence intervals will be wrong, but with a larger sample size the estimate will be closer to the true error-estimate. What you need to justify instead is whether a model that is based only on a conditional mean is a good representation of your situation with an ordinal variable. – Sextus Empiricus Apr 09 '21 at 16:23
  • Thank you for your comment. Could you elaborate why the standard errors would be wrong if I satisfy all CLM assumptions? Because that is what I don't really get. Could you also elaborate perhaps on how I determine whether a model based on only a conditional mean is a good representation, and what better options might be? – Tom Apr 09 '21 at 16:28
  • 1
    By characterizing the response as ordinal, you are telling us its numerical values have no inherent meaning: the only information they reflect is relative ordering. Thus, *it doesn't even make sense* to compute a residual or discuss the distribution of residuals. This problem can be resolved by finding a meaningful way to encode the response values numerically--but that's not the only method. See our [posts on ordinal regression](https://stats.stackexchange.com/search?q=ordinal+regression). – whuber Apr 09 '21 at 17:09
  • @whuber Thank you for your comment. Any chance you could elaborate on "finding a meaningful way to encode the response variables numerically"? (I am going through the posts on ordinal regression as we speak.) – Tom Apr 09 '21 at 17:25
  • @whuber One more thing, is there any method to prove or make it reasonable to assume that the difference between the levels are equivalent? – Tom Apr 09 '21 at 17:27
  • First, this is a big subject. Historically it was discussed in papers like Lord's famous discussion of football numbers. See https://stats.stackexchange.com/a/106400/919 for an overview and a reference (the paper is freely available online). Second, there are indeed such methods. In fact, that's what many techniques of ordinal regression attempt to accomplish: they simultaneously find numerical cutpoints to separate the ordinal classes and fit a regression. – whuber Apr 09 '21 at 17:29
  • @whuber I'm really thankful for your comments. But I notice that I am finding it hard to generate a next step from what you are saying. I have been dealing with this issue for quite a while. Is there any way you could be a little bit more specific in what I could try? The problem is that most answers I find, result in simply saying: "use ordinal" and it's hard to find things that specifically relate to my case, where I cannot really use ordinal for a different reason. – Tom Apr 09 '21 at 17:36
  • It would help to explain what you think the limitation to using ordinal regression might be. It seems to derive from a strategy you have developed to solve a bigger problem -- so maybe you ought to be rethinking this strategy instead of trying to jury-rig a solution involving ordinary least squares. – whuber Apr 09 '21 at 17:59
  • There is a link in my question, which deals with this "why": https://stats.stackexchange.com/questions/518535/how-to-get-residuals-from-an-ordinal-logit-probit-and-which-ones-to-get. I have also already tried to address that part as well, without much success. Just to be clear, it does not need to be OLS. It just needs to be a regression that produces residuals. – Tom Apr 09 '21 at 18:05
  • I'm really trying this from every angle.. But every time I get stuck somewhere. – Tom Apr 09 '21 at 18:08

0 Answers0