I know qnorm() function returns the z-statistic of the applicable normal distribution that corresponds to a given probability (see example below).
qnorm(p = 0.75, mean = 0, sd = 1, lower.tail = T)
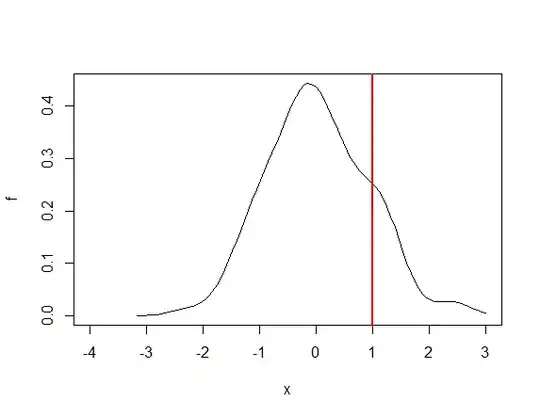
What I am looking for is a way to do the same but for a custom distribution that I have estimated using the density() function in base R. The probability density function of my custom distribution has been approximated using approxfun(). See below example. I am interested in a way to get the x-axis value corresponding to some lower tail (alternatively upper tail) probability of my choice. In the figure below I have added a red line at x= 1 to illustrate what i mean: assume that P(X<x=1) = 0.75 in the figure below - Is there a way for me to find out that x = 1 is the value on X that yields P(X<x) = 0.75?
set.seed(0)
x <- rnorm(n = 100, mean = 0, sd = 1) # Generate a reproducible RV
f <- approxfun( density(x) ) # This is my approximated PDF
plot(f, -4, 3)
abline(v = 1, col = "red", lw = 2)