I had already read some interesting alternatives to interpret the plot(mymodel) from a gam fit like in this answer.
# Data
dd <- structure(list(GDP = c(30515, 19725, 35894, 17305, 9867, 15214,
43142, 13934, 56774, 25288, 44636, 28935, 43253, 23625, 25837,
31116, 27862, 16556, 16190, 25195, 14986, 68933, 26267, 20440,
21746, 14986, 30447, 21710, 42224, 15095, 16263, 25024, 31002,
32848, 43761, 33176, 13792, 23625, 16808, 41057, 37892, 20492,
34935, 29958, 34454, 73465, 18060, 39449, 25776, 31777, 46402,
15623, 29712, 21008, 36198, 25024, 33176, 18778, 41175, 25024,
31988, 17725, 24179, 13504, 77617, 14269, 26825, 24375, 16580,
44448, 19523, 24515, 25039, 16730, 37844, 16318, 62974, 20693,
16810, 18255, 30614, 27727, 16611, 23625, 35383, 20355, 36502,
50673, 24552, 30495, 20492, 11768, 14413, 20120, 44398, 23072,
19668, 25189, 16355, 37361, 27216, 28597, 45313, 27216, 19653,
76194, 11902, 34292, 36800, 18778, 57664, 60916, 29712, 18368,
11611, 14280, 34631, 12135, 27737, 23825, 35751, 44606, 32497,
15095, 29658, 31021, 21209, 10060, 15132, 47559, 44835, 27081,
31777, 11442, 39756, 12565, 16093, 25794, 58756, 24383, 23815,
22555, 9073, 23031, 34812, 25895, 13934, 36892, 28638, 12606,
31116, 17963, 25749, 23072, 29509, 44835, 46843, 12285, 18688,
30305, 43761, 50624, 24515, 27595, 21799, 17298, 25794, 19425,
18868, 26779, 32437, 25438, 43253, 15523, 20436, 29302, 41583,
38833, 44443, 20324, 18578, 36462, 23329, 14269, 15479, 15214,
17465, 19704, 13305, 23075, 32776, 15623, 10918, 44587, 24671,
8478, 11442, 33828, 35383, 27749), Wage = c(0, 21897.3005962264,
18098.1013668886, 5721.51105263158, 0, 0, 0, 14376.0889184, 38547.9376727447,
17722.3549873251, 17110.1706479156, 0, 142309.937, 0, 0, 42446.4695569812,
0, 9613.13095508445, 0, 0, 4141.19977411764, 17680.2982901078,
23437.8599580815, 0, 0, 26661.2739361382, 21078.9864430457, 0,
70395.4781485715, 0, 0, 39602.1593640719, 21353.1996631231, 0,
0, 31263.1240312159, 0, 0, 16742.3629381408, 30609.4028735632,
0, 0, 143039.443786666, 11689.0115524349, 37346.9720513089, 160378.6592375,
0, 0, 0, 27964.3515373334, 4435.205225, 0, 23691.7178206271,
10859.1139584504, 30671.1090078788, 0, 30790.622685, 0, 22302.4321223963,
7951.11867047619, 0, 7171.93619768519, 66602.2565076336, 0, 104196.074399216,
0, 15442.7193010811, 23293.1851001307, 0, 0, 25831.393328, 0,
21359.02725, 0, 8050.588616, 16338.1106, 2579.6373062069, 0,
15948.3485306372, 0, 20361.5500836544, 31677.6394032, 0, 12564.0154095238,
35821.580462963, 36947.9503866666, 25300.8266651163, 45732.7877231373,
0, 0, 0, 0, 0, 20482.8640638462, 12747.1747921875, 41477.654,
0, 23700.4572205275, 0, 0, 20606.6365738378, 0, 16877.7788716709,
18479.6474883721, 0, 2633.61414059406, 0, 31657.6492790697, 212166.588333333,
0, 35460.0238402204, 3868.9808, 0, 0, 0, 0, 0, 0, 0, 0, 22129.6907649569,
30046.8504292683, 14410.4145120514, 0, 0, 0, 0, 0, 0, 11575.0498309424,
39037.0514451477, 0, 29708.3057267846, 25378.712632653, 0, 0,
16621.9704982911, 39704.0317835294, 0, 14930.805379836, 43284.495181337,
0, 0, 0, 15037.2481154986, 0, 16921.2017315598, 19875.7748910244,
21389.2608662444, 0, 135229.170095384, 0, 0, 22787.2578523466,
14343.1388662444, 16381.7273025584, 33001.9426123596, 20879.5439641899,
0, 0, 21767.370135849, 29353.1834862035, 22868.1726857143, 19266.8150472126,
15907.7118561494, 14654.5679873171, 24638.5213278535, 290769.262608,
0, 14570.2077740541, 22646.471631356, 0, 95517.8176422765, 19878.7632243161,
14698.958974353, 24720.8489643781, 28625.2423755036, 32259.2125263604,
28017.9849961773, 0, 13508.1738694762, 29150.2506749763, 0, 17556.1824878261,
0, 0, 0, 0, 0, 15584.3064931477, 31537.3301848598, 0, 0, 0, 17668.4740558409,
0, 23652.4630510345, 120560.601746666, 0, 0), Impostos = c(258226.676256,
7666065, 3109820.88922, 0, 0, 0, 0, 1422423.021272, 4934817.705125,
1483048.940481, 7077441.931609, 5820.292305, 222079.463375, 659.22175,
83585.1555, 320840.867347, 12152.633423, 1539360.423536, 9581.325835,
111399.905589, 0, 21796324.291819, 2928394.5999, 17332.849282,
2498.140128, -573250.033617, 1157166.42008, 15769.690384, 421808.68674,
0, 183157.899205, 3328234.468041, 5682789.587699, 5006.299375,
18268.75023, 104737934.0823, 33089.171395, 2791.401448, 1556758.5678,
0, 111876.46437, 121321.9722, 258226.676256, 2414974.36635, 916062.9081,
1975036.28904, 1561224.230828, 0, 0, 0, 454954.02975, 31272.05675,
5084207.455964, 2422543.905098, 1724820.238501, 397492.156583,
0, 0, 5755422.61052, 0, 0, 1034.491323, 3530226.1995, 0, 1124309.586451,
0, 874523.528256, 269120.645112, 4328.002768, 2552.270875, 3640.803141,
40462.97585, 199884.6179, 573.356233, 40544.727907, 72871.686048,
206343.844042, 75328.7612, 470901.68573, 692158.443962, 5587374.731822,
0, 232664.557057, 123364.091224, 2019102.652875, 2170.593684,
1265.561115, 328343.671061, 50817.086913, 0, 70457.29152, 2094.3065,
111137.169717, 121950.321528, -116001.32229, 3725.8628, 0, 6175891.538784,
0, 0, 12252018.137656, 5556.082658, 33425581.032815, 6148657.88515,
341115.8817, 199270.51344, 1034010.912088, 5164601.75, 0, 32833.799152,
6983242.94025, 391597.461504, 209116.513305, 3995.909141, 0,
5130.959856, 501898.121985, 0, 218487.286927, 19818.939585, 6300922.482113,
1054770.174555, 26308690.90355, 0, 454761.440923, 19771.560761,
9190.036619, 0, 90784.561846, 4743249.903283, 1510454.994125,
0, 91898751.0203, 0, 0, 0, 1023339.879699, 831.7556, 31683.9215,
5400542.827929, 4912558.07262, 1255764.09219, 72295.526989, 1576276.2015,
31291270.907688, 8543.72812, 332443.0835, 832474.902846, 3174089.285538,
42774.207855, 111399.905589, 83105.83931, 22407.841904, 62756859.66,
5031482.235648, 2850166.33825, 444017.09275, 1049166.784934,
24371.831533, 279939.808095, 250419.056385, 7294100.376346, 173702.71985,
6123401.138575, 2852782.779528, 617556.403032, 50243018.9536,
0, 4000.7068, 614062.662561, 517729.799125, 11713.290821, 558763.695875,
178316.056032, 175401.966415, 356368.180205, 13540021.831425,
1919305.031347, 11104163.28175, 5738.614963, 1853842.915983,
9680024.6557, 10546.207868, 175374.182494, 519945.056939, 0,
120.188278, 0, 1324929.539352, 926744.526451, 667209.782967,
6392.842544, 0, 54088.93473, 2155260.814341, 349.713712, 3573533.041848,
191109.153862, 347176.339125, 191109.153862)), row.names = c(480L,
127L, 454L, 156L, 152L, 173L, 342L, 208L, 571L, 485L, 313L, 549L,
578L, 176L, 587L, 317L, 365L, 69L, 111L, 358L, 95L, 323L, 307L,
349L, 243L, 62L, 187L, 366L, 500L, 166L, 282L, 306L, 253L, 610L,
542L, 373L, 53L, 237L, 63L, 553L, 548L, 154L, 456L, 332L, 499L,
524L, 466L, 609L, 460L, 407L, 181L, 183L, 328L, 80L, 381L, 401L,
468L, 168L, 205L, 400L, 408L, 77L, 563L, 105L, 402L, 42L, 363L,
198L, 417L, 603L, 102L, 171L, 134L, 107L, 479L, 31L, 364L, 175L,
20L, 422L, 379L, 346L, 118L, 209L, 560L, 41L, 529L, 36L, 471L,
426L, 215L, 162L, 32L, 26L, 525L, 163L, 533L, 188L, 350L, 159L,
192L, 336L, 247L, 131L, 179L, 547L, 222L, 551L, 577L, 229L, 510L,
303L, 354L, 60L, 44L, 457L, 545L, 112L, 362L, 539L, 314L, 503L,
125L, 227L, 423L, 412L, 478L, 91L, 99L, 266L, 555L, 37L, 312L,
136L, 281L, 33L, 269L, 285L, 601L, 268L, 502L, 544L, 56L, 588L,
186L, 488L, 147L, 453L, 267L, 122L, 334L, 287L, 351L, 129L, 191L,
576L, 564L, 86L, 49L, 415L, 514L, 327L, 133L, 318L, 196L, 302L,
190L, 272L, 121L, 270L, 607L, 477L, 561L, 67L, 87L, 259L, 497L,
442L, 558L, 279L, 74L, 429L, 355L, 6L, 361L, 234L, 356L, 277L,
283L, 65L, 320L, 244L, 289L, 534L, 264L, 106L, 197L, 395L, 598L,
419L), class = "data.frame")
I have a gam model with Gamma link function:
library(mgcv)
m2 <- gam(GDP ~ s(Wage) +
s(Impostos),
data = dd,
select = T,
family = Gamma(link = "log"),
method = "REML")
And I plot it:
plot(m2, shade = T, se = T, select = 1,
xlab = "Wage",
ylab = "Change in log of GDP")
I usually interpret as:
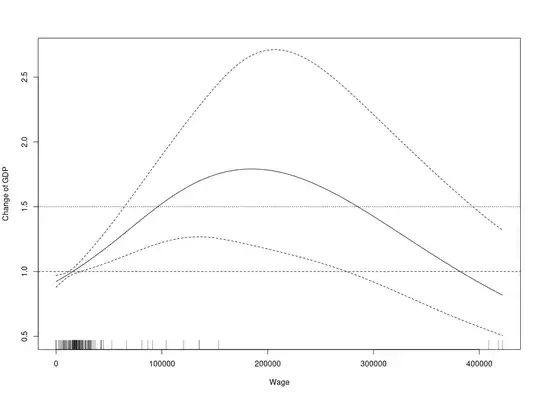
Up to Wage 200000 there is an increase in the log of GDP, and after that a decrease up to 300000, and after that, there is no change (because 0 crosses the shaded area).
However, can I say how much is the increase? Like, up to Wage 200000 there is an increase in the log of GDP of a little bit more than .5 (value in the y-axis) compared to Wage around 1500 ? (hard to tell by the scale of the graphic if the Wage that crosses 0 on y-axis is 1500) I am looking for interpretation-like regression coefficients.
If I exponentiate my y-axis I would get:
plot(m2, shade = T, se = T, select = 1,
trans = exp,
xlab = "Wage",
ylab = "Change of GDP")
Can I say that up to Wage 100000 there is an almost 50% increase (compared to low value of Wage that on y-axis crosses 1)?
Addition (1): Added graphics with log1p(Wage)
The results are still weird because at least 40% of the data is zero:
> quantile(dd$Wage, probs = seq(0,1,.1))
0% 10% 20% 30% 40% 50% 60% 70%
0.00 0.00 0.00 0.00 0.00 8831.86 16355.56 21161.25
80% 90% 100%
25997.37 36987.85 290769.26
Maybe should I do something else?
m2 <- gam(GDP ~ s(log1p(Wage)) +
s(Impostos),
data = dd,
select = T,
family = Gamma(link = "log"),
method = "REML")
plot(m2, shade = T, se = T, select = 1,
xlab = "Wage",
ylab = "Change in log of GDP")
plot(m2, shade = T, se = T, select = 1,
trans = exp,
xlab = "Wage",
ylab = "Change in log of GDP")
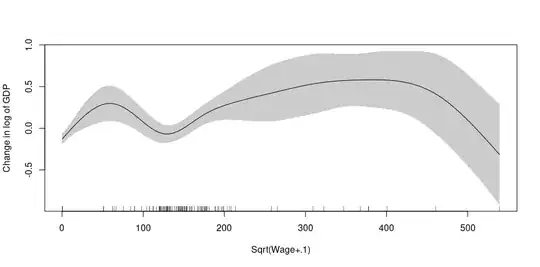
Addition (2): Added graphics with sqrt(Wage+.1)
m2 <- gam(GDP ~ s(sqrt(Wage+.1)) +
s(Impostos),
data = dd,
select = T,
family = Gamma(link = "log"),
method = "REML")
plot(m2, shade = T, se = T, select = 1,
xlab = "Sqrt(Wage+.1)",
ylab = "Change in log of GDP")
plot(m2, shade = T, se = T, select = 1,
trans = exp,
xlab = "Sqrt(Wage+.1)",
ylab = "Change of GDP")
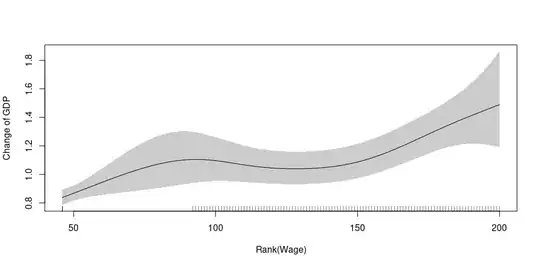
Addition (2) : Added graphics with rank(Wage)
Note how the interpretation changes in the end compared to the first graphic. It happens because the extreme values join with the less extreme values. I don't know how usual it is this, but I think that it is an option.
The %Dev. Explained with only s(rank(Wage)) is 19.6%, with s(Wage) is 16.2%, s(log(Wage+.1)) is 15.3% and s(sqrt(Wage+.1)) is 21.5%. I am not sure if I should change the transformation based on the %Dev. Explained (I think that it may help).
m2 <- gam(GDP ~ s(rank(Wage)),
data = dd,
select = T,
family = Gamma(link = "log"),
method = "REML")
plot(m2, shade = T, se = T, select = 1,
xlab = "Rank(Wage)",
ylab = "Change in log of GDP")
plot(m2, shade = T, se = T, select = 1,
trans = exp,
xlab = "Rank(Wage)",
ylab = "Change of GDP")
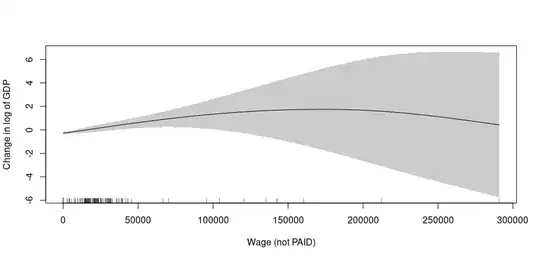
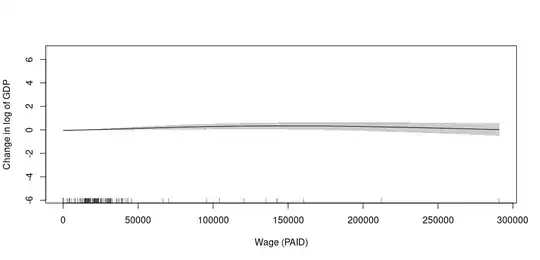
Addition (3): Added graphics with s(Wage, by = PAID) WITH % Dev. explained = 18.4%
dd$PAID <- factor(with(dd, Wage>0),
labels = c("Não", "Sim"),
levels = c(F,T))
levels(dd$PAID)
"Não" "Sim"
m2 <- gam(GDP ~ s(Wage, by = PAID),
data = dd,
select = T,
family = Gamma(link = "log"),
method = "REML")
plot(m2, shade = T, se = T, select = 1,
xlab = "Wage (not PAID)",
ylab = "Change in log of GDP")
plot(m2, shade = T, se = T, select = 2,
xlab = "Wage (PAID)",
ylab = "Change in log of GDP")
What I did not understand from this transformation, was that the smooth was made for all range of Wage even for those who are not PAID. And for those who were PAID, there is no effect at all