Problem with parallel analysis with psych

Question

I have a data set with several hundred variables and some thousand records. I'm reviewing the different ways for running a Principal Component Analysis and choosing the principal components.

First I used the function prcomp() to get the advantage of using SVD. The first component explains more than 50% of the variance and the second a % more. The remaining components are very small.

This is the figure I got:

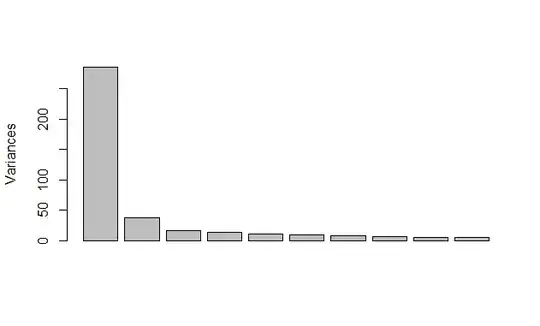
Then, by reading some posts here in Cross Validated I found that a recommended method for choosing the principal components was the so called "parallel analysis" and 2 libraries were recommended including the psych.

So I decided to try that method. This is the code I used:

> fa.parallel(my.dataframe,
          fa="PC", 
          n.iter=100,
          how.legend=FALSE, 
          main="My Plot")

I received the following results in the command prompt:

Loading required package: MASS
In smc, the correlation matrix was not invertible, smc's returned as 1s
In smc, the correlation matrix was not invertible, smc's returned as 1s
The determinant of the smoothed correlation was zero.
This means the objective function is not defined.
Chi square is based upon observed residuals.
The determinant of the smoothed correlation was zero.
This means the objective function is not defined for the null model either.
The Chi square is thus based upon observed correlations.
In factor.stats, the correlation matrix is singular, an approximation is used
In factor.scores, the correlation matrix is singular, an approximation is used
I was unable to calculate the factor score weights, factor loadings used instead
Parallel analysis suggests that the number of 
    factors =  54  and the number of components =  44 
Warning messages:
1: In cor.smooth(R) : Matrix was not positive definite, smoothing was done
2: In cor.smooth(R) : Matrix was not positive definite, smoothing was done
3: In cor.smooth(r) : Matrix was not positive definite, smoothing was done
4: In factor.stats(r, loadings, Phi, n.obs = n.obs, np.obs = np.obs,  :
  In factor.stats, the correlation matrix is singular, and we could not calculate
      the beta weights for factor score estimates
5: In cor.smooth(r) : Matrix was not positive definite, smoothing was done

And this is the resulting figure:

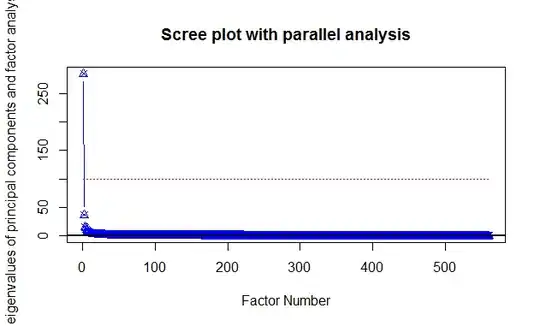
None of the PCA figures I had reviewed look like this, and I'm totally lost at analyzing its significance. I guess I should choose the first 44 principal components.

I'd really appreciate if somebody could explain this to me a little bit.

Answer 1

Parallel analysis is implemented for R in the paran package available on CRAN here.

The basic logic behind parallel analysis is to improve upon the eigenvalue > 1 (principal component analysis) or eigenvalue > 0 (common factor analysis), by (1) recognizing that in finite data, some eigenvalues will be greater than 1 or less than 1 simply due to chance because the correlation matrix will not be a perfect identity matrix, and (2) correcting for this "sampling and least squares bias" by averaging the each of the p eigenvalues from "many" uncorrelated data sets of the same n and p as your observed data, and retaining only those observed eigenvalues greater than the corresponding mean of random data eigenvalues.

You might also be interested in reading the document Gently Clarifying the Application of Horn’s Parallel Analysis to Principal Component Analysis Versus Factor Analysis which is linked to within the documentation for paran.