Predict background counts given past observations and assumption of linear variation of the rate parameter in time

Question

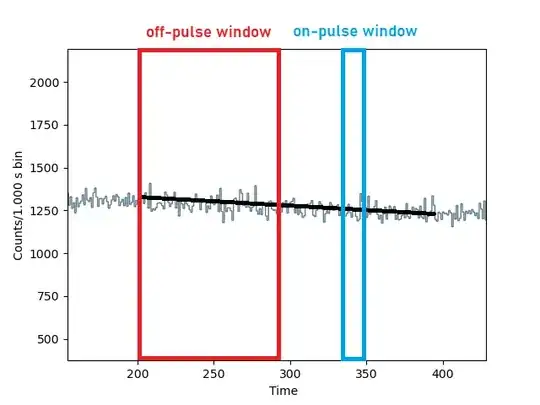
Consider the following problem. We have a time series of counts (poisson-distributed) data. In this time series we can select an off-pulse window in which only background is present and a subsequent on-pulse window in which a source signal may or may not be present.

I want to estimate a mean value and error for the background counts in the on-pulse window $b = b \pm \sigma$, given the off pulse observations and the assumptions that the poisson rate can change linearly $\sim mt + q$.

The actual situation is depicted in the following picture. A paper I'm studying claims that $b$ should be normally distributed with good approximation, even when $b$ is small.

This looks as a fairly straightforward problem which I don't how know to approach. If data were gaussian distributed and error bars were given, a linear regression would do the trick. In particular, i would estimate $m \pm \sigma_m$ and $q \pm \sigma_q$ and propagate their errors.

Where should I look?

One remark: i'm particularly interested in the case in which on-pulse window is small (few counts).

Answer 1

You have a Poisson point process with intensity (rate) function $\lambda(t)$, say. Assume the observation window is contained in the interval $[0, T]$ and the observed points $t_1, t_2, \dotsc, t_n$. Let $N(T)$ be the total count of points. Then we can show that $$ N(T) \sim \mathcal{Poisson}\left( \int_0^T \lambda(t)\; dt \right) $$ and there is the following Theorem: (See Pawitan, In All Likelihood (reference in here: Manipulating Binomial Distribution)): Given $N(T)=n$, the times $t_1, t_2, \dotsc, t_n$ are distributed as the order statistics of an iid sample from a distribution with density proportional to $\lambda(t)$. Introducing $\Lambda(T)=\int_0^T \lambda(t)\; dt$ this density is $$\frac{\lambda(t)}{\Lambda(T)} $$ Denoting by $\theta$ unknown parameters in the intensity function, we can now find the likelihood function for $\theta$: $$ \DeclareMathOperator{\P}{\mathbb{P}} L(\theta)= \P\left(N(T)=n\right)\cdot \P(t_1, t_2, \dotsc, t_n | N(T)=n) \\ = e^{-\Lambda(T)} \frac{\Lambda(T)^n}{n!}\times n! \prod_1^n \frac{\lambda(t_i)}{\Lambda(T)} \\ = e^{-\Lambda(T)} \prod_1^n \lambda(t_i) $$ and using your assumption on the intensity function and the two windows, you can take it from here, using maximum likelihood estimation.