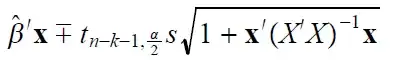1

I came across this great tutorial, which shows how to compare/visualise main effect of logistic regression GLMs (apart from other things). All independent variables appear to be numeric and are thus scaled (z-scored). This allows a great comparison of the impacts of the main effects:

enter image description here

When I apply this methodology to my data, which also contains factors, the factors estimates are quite large. Do I have to explicitly introduce dummy variables (which would be 0 or 1) or how do I make the estimates of my dummy variables comparable with the scaled numeric variables? Thanks!

cs0815
  • 1,294
  • 18
  • 30
  • 1
    This is called a forest plot. For a logistic regression, we usually exponentiate the effects. The $p<0.05$ is not correct because it's not controlling for multiple testing, and should be removed. Plus you can simply look at whether the 95% CI bars cross the null value at 0 (or 1). Lastly, it's rarely of interest to plot multiple unrelated factors in a forest plot such as this. – AdamO Feb 12 '21 at 18:08
  • Thanks. I just took this from the blog post. – cs0815 Feb 12 '21 at 21:03

1 Answers1

2

The issue is that the units of the $X$-variables are not constant, so standardizing them makes them the same (at least in the sense of all being standard deviations—whether that really makes them the same is a bit of a philosophical issue).

You are discussing this in terms of variable , but the topic has been discussed extensively in the area of penalized estimation methods (i.e., ridge, LASSO, and elastic net regression). Hastie and Tibshirani have argued that you should standardize your dummy variables as well. If your factor is perfectly 50-50, this will output essentially $-1$ and $1$ as the new values; if it's unbalanced, it will shift towards $-\infty$ and $0$ or $0$ and $\infty$, depending on whether your (current) $0$'s or $1$'s are more prevalent, how imballanced they are, and how many data you have. This gets trickier if you have multi-category categorical variables. It may help you to read these threads:

A different way to visualize variable importance with a mix of categorical and continuous variables is to get a variable's chi-squared statistic from its likelihood ratio test and divide that by its degrees of freedom.

lrts = drop1(glm(Solea_solea ~ ., family="binomial", data=Solea), test="LRT")
## in this case, all variables have 1 df, so the division is a waste of time, 
##  but in other contexts, you could do:  
lrts$importance = with(lrts, LRT/Df)
lrts
#               Df Deviance    AIC    LRT Pr(>Chi) importance
# <none>             51.830 77.830                           
# Sample         1   53.762 77.762 1.9314  0.16461     1.9314
# season         1   52.101 76.101 0.2711  0.60259     0.2711
# month          1   53.341 77.341 1.5107  0.21903     1.5107
# Area           1   58.696 82.696 6.8660  0.00879     6.8660
# depth          1   51.957 75.957 0.1273  0.72125     0.1273
# temperature    1   51.922 75.922 0.0918  0.76190     0.0918
# salinity       1   55.457 79.457 3.6269  0.05685     3.6269
# transparency   1   52.125 76.125 0.2953  0.58688     0.2953
# gravel         1   51.834 75.834 0.0039  0.95020     0.0039
# large_sand     1   51.834 75.834 0.0041  0.94922     0.0041
# med_fine_sand  1   51.834 75.834 0.0043  0.94800     0.0043
# mud            1   51.834 75.834 0.0041  0.94888     0.0041
gung - Reinstate Monica
  • 132,789
  • 81
  • 357
  • 650
  • Actually, since the OP claims the variables are factor encoded, we (might?) assume they're typical 0/1 encodings. In that case, the three possibilities to consider are: a) singular estimates from the GLM / small sample bias, b) the effect size is just really freaking huge for some effects (not others), c) the sample size is so large the "forest plot" shows up like disparate little points. – AdamO Feb 12 '21 at 18:06
  • @AdamO, they certainly start off as typical 0/1 encodings, but you can standardize those vectors just as you do for continuous variables. As for the rest of your points, yes. – gung - Reinstate Monica Feb 12 '21 at 18:15
  • I just just used factors, which can have more than 2 levels. Should I introduce explicit dummies first? Dummies would be 0 or 1. Do they have to be - 1 – cs0815 Feb 12 '21 at 21:07
  • @cs0815, R will be making dummies for you behind the scenes. If you have >2 levels, it gets complicated & you have to make some choices. I'm not a fan of variable importance in the first place, I would recommend against this procedure. If you need something, I would divide the chi-squared statistic from the likelihood ratio test by its degrees of freedom. That gives you a measure of importance that accounts for the fact that some variables have multiple levels. – gung - Reinstate Monica Feb 12 '21 at 21:21
  • Thanks. Yes that's what I thought reg. dummies and lm glm type models. Yes I agree. I heard of the likelihood ration test etc. Are you aware of a good R example/tutorial? Thanks. – cs0815 Feb 12 '21 at 21:29
  • Sorry is it as simple as you showed then? Is multiple testing an issue? – cs0815 Feb 12 '21 at 21:46
  • @cs0815, well, I posted example code based on the linked tutorial in my answer... – gung - Reinstate Monica Feb 12 '21 at 21:46
  • @cs0815, this isn't a test, it's just a ranking. I wouldn't necessarily take the results as gospel if 2 variables end up with similar numbers. – gung - Reinstate Monica Feb 12 '21 at 21:48
  • OK afik true statisticians would not rank and potentially throw away IVs. I am looking at a dataset with 100 plus IVs and wanted something to help me focus and use something else than random forest feature importance. Besides I want to use GLMs hierarchical models more. Thanks – cs0815 Feb 12 '21 at 21:53