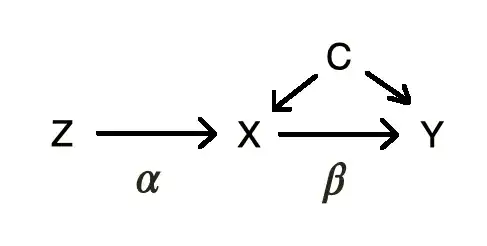An intuitive explanation of the instrumental variable

Question

This is something that I had dealt with in my MSc Economics many years ago, passed the exams with flying colours, yet when I thought about it in more depth today, I was somewhat puzzled. This could perhaps be because it's been a couple of years since I last covered the topic, or maybe it is due to the fact that I had only learnt the theory and never dealt with a practical example; regardless some intuitive explanation, strengthened with a mathematical proof would be very much appreciated.

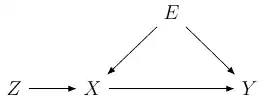
The general idea is that for $y=\beta'x+\varepsilon$, the exogeneity assumption must hold -i.e. $\mathbb{E}\{x(y-\beta'x)\}=0$. When this assumption is violated -i.e. $\mathbb{E}\{x(y-\beta'x)\}\neq0$, we find an instruments $z$, such that $\mathbb{E}\{z(y-\beta'x)\}=0$, while $\mathbb{E}\{xz\}\neq 0$. In other words, $x$ and $z$ are correlated, but while $x$ is correlated with $\varepsilon$, $z$ is not! I cannot see how this could be the case. Or does the assumption has more to do with "perfect" collinearity? As in $z$ would still be correlated with $\varepsilon$, but not to the same extent that $x$ is? Thank you!

Answer 1

I think the most intuitive explanation lies in the causal Directed Acyclic Graph (DAG) approach taken by Judea Pearl, where $A\to B$ means $A$ causes $B$. The typical setup for an instrumental variable is as follows:

Here the unmeasured variable $E$ is your variable causing the problem, because it sets up a backdoor path from $X$ to $Y,$ and is thus a true confounder. You cannot condition on it because it is unmeasured. So you find an instrumental variable $Z$ that causally affects only $X$, and has no causal effect on $E$ or $Y$ in either direction. The reason $Z$ and $E$ can be uncorrelated is that if you examine the path $Z\to X\leftarrow E,$ the collider at $X$ prevents causal information flow from $Z$ to $E.$ Similarly, if you examine the path $Z\to X\to Y\leftarrow E,$ the collider at $Y$ prevents information flow. There are no other paths from $Z$ to $E,$ so there can be no information flow from $Z$ to $E$ or vice versa.

Incidentally, it is also sometimes possible to correct for $E$ using the frontdoor approach. If you can insert a variable $Z$ in-between $X$ and $Y$ thus:

Then you can invoke the frontdoor adjustment formula: $$P(Y|\operatorname{do}(X))=\sum_zP(Z=z|X)\,\sum_xP(Y|X=x, Z=z)\,P(X=x).$$ This is not always possible, unfortunately.

Answer 2

I also struggled with intuitive understanding of IV method. There are few explanations, which are worth considering. Let me present you the one I found by myself, which is for me quite convincing.

First, for me DAG paradigm perfectly described by @Adrian Keister is the key to understand what is going on here. It helps to both understand exclusion restriction assumption, as well as other variants of instruments described in Brito and Pearl (2012).

Causal graphs in convenient way introduce mediation. Lets look at the classical causal model for instrumental variable in terms of mediation:

Effect we want to identify is $\beta$, it is "true" effect of X on Y. As described in previous answer, it can not be identified directly, because of existence of unmeasured confounder C.

However we can understand it in a way, that X mediates effect of Z on Y.

In this setting effect Z on X is identified correctly, it is equal $\alpha$. Also, effect of Z on Y is identified correctly, it is equal $\alpha \cdot \beta$.

Therefore if we want to calculate $\beta$ we can simply divide estimator from the second model by estimator from the first model. The procedure would be similar, as in estimating the effect in front-door criterion.

What happens then in the 2SLS procedure? In my intuitive understanding we still estimate still effect of Z on Y, however it includes already forced, or already included $\alpha$ parameter. What is left in the second stage regression is only $\beta$.

---

Brito, Carlos, and Judea Pearl. "Generalized instrumental variables." arXiv preprint arXiv:1301.0560 (2012).