4

I have a large sample (a vector) $\mathbf{x}$ from a random variable $X\sim N(\mu,\sigma^2)$. The variance $\sigma^2$ is known, but the expectation $\mu$ is unknown. I would like to test the null hypothesis $H_0\colon \ \mu=0$ against the alternative $H_1\colon \ \mu>0$ using a likelihood ratio (LR) test. The test statistic is $$ \text{LR}=-2\ln\frac{L(\mathbf{x}\mid 0,\sigma^2)}{L(\mathbf{x}\mid\hat\mu,\sigma^2)}. $$ where $\hat\mu$ is the estimate of $\mu$ under $H_0 \cup H_1$ (thus $\hat\mu\geq0$).

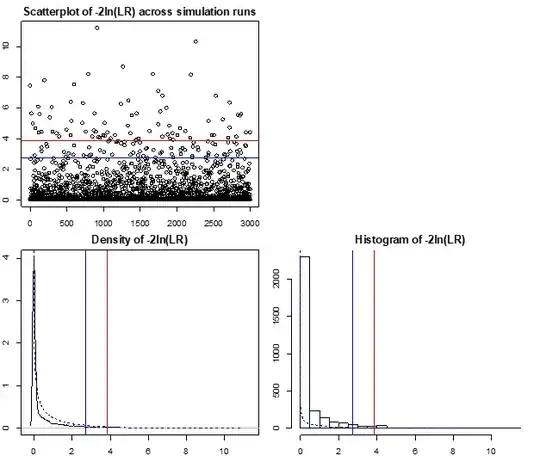
I expected the asymptotic distribution of $\text{LR}$ under $H_0$ to be $\chi^2(1)$ but I am getting something else in a simulation below.

Questions: Why is that? Is my simulation wrong? Or is the test statistic not supposed to have the $\chi^2(1)$ asymptotic distribution under $H_0$, and if so, why?

(Related question: "Failing to obtain $\chi^2(1)$ asymptotic distribution under $H_0$ in a likelihood ratio test: example 2")

n=3e3   # sample size
sigma=1 # standard deviation of X
m=3e3   # number of simulation runs

logL0s=logL1s=logLRs=rep(NA,m)
for(i in 1:m){
 set.seed(i); x=rnorm(n,mean=0,sd=sigma)
 logL0=sum(log( dnorm(x,mean=0,sd=sigma) ))
 logL1=sum(log( dnorm(x,mean=max(0,mean(x)),sd=sigma) ))
 logLR =-2*(logL0-max(logL0,logL1)) # the -2*ln(LR) statistic from this simulation run
 logL0s[i]=logL0; logL1s[i]=logL1; logLRs[i]=logLR
}

# Critical values: asymptotic nominal vs. empirical
crit.val=qchisq(p=0.95,df=1)
empirical.crit.val=quantile(x=logLRs,probs=0.95)
print(paste0("Asymptotic critical value = ",round(crit.val,2),", simulated critical value = ",round(empirical.crit.val,2)))

# Test size: asymptotic nominal vs. empirical
empirical.size=length(which( logLRs > crit.val ))/m # proportion of rejections at 0.05 level
print(paste0("Nominal test size = 0.050, simulated test size = ",round(empirical.size,3)))

# Plots illustrating the sampling distribution of -2*log(LR) statistic
par(mfrow=c(2,2),mar=c(2,2,2,1))
 plot(logLRs,main="Scatterplot of -2ln(LR) across simulation runs")
  abline(h=crit.val,col="red")
  abline(h=empirical.crit.val,col="blue")
 plot(NA)
 plot(density(logLRs),main="Density of -2ln(LR)")
  chisq.quantiles=qchisq(p=seq(from=0.001,to=0.999,by=0.001),df=1)
  chisq.density=dchisq(x=chisq.quantiles,df=1)
  lines(y=chisq.density,x=chisq.quantiles,col="blue",lty="dashed")      # Chi^2(1) overlay
  abline(v=crit.val,col="red")                                          # asympt. nominal crit. val. in red
  abline(v=empirical.crit.val,col="blue")                               # empirical crit. val. in blue
 br=24
 hist(logLRs,breaks=br,main="Histogram of -2ln(LR)")
  lines(y=chisq.density*m/br,x=chisq.quantiles,col="blue",lty="dashed") # Chi^2(1) overlay
  abline(v=crit.val,col="red")                                          # asympt. nominal crit. val. in red
  abline(v=empirical.crit.val,col="blue")                               # empirical crit. val. in blue
par(mfrow=c(1,1))

enter image description here

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
  • Related: ["Asymptotic null distribution of the LR statistic with point null and point alternative"](https://stats.stackexchange.com/questions/506750). – Richard Hardy Jan 27 '21 at 12:33
  • Related: ["What are the regularity conditions for Likelihood Ratio test"](https://stats.stackexchange.com/questions/101520). – Richard Hardy Jan 27 '21 at 12:33
  • You are on the boundary of the parameter space: the result you are relying on doesn't hold in such cases. Typically the distribution of the LR is a mixture of chi-squared distributions. – whuber Jan 27 '21 at 14:31
  • @whuber, thank you so much! I was suspecting it, but I got confused about the definition of the parameter space. Is the parameter space defined by $H_0 \cup H_1$, so in my case, $\mu\in [0,\infty)$? – Richard Hardy Jan 27 '21 at 14:34
  • Yes: this became clear to me when I saw you force $\hat\mu$ to be non-negative in your code at `max(0,mean(x))`. – whuber Jan 27 '21 at 14:57
  • @whuber, well, I was just trying to follow the definition of the LR statistic. Should I have used unrestricted estimation instead? I think that would be at odds with the definition of the denominator in the LR formula. – Richard Hardy Jan 27 '21 at 15:02

1 Answers1

3

Apparently the test statistic not supposed to have the $\chi^2(1)$ asymptotic distribution under $H_0$. Thanks to @whuber for pointing this out.

The example violates an assumption for the distribution to be $\chi^2(1)$. The assumption is that the parameter of interest in not on the boundary of the parameter space. I am not entirely sure how the parameter space is defined, but it seems it is defined by $H_0\cup H_1$. In my case this would mean $\mu\in [0,\infty)$. Now $\mu=0$ due to $H_0$ is on the boundary of $[0,\infty)$, so that constitutes a violation.

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219