What is "likelihood-based LDA" and "likelihood-based QDA", how do they relate to LDA and QDA, and how they are implemented in R?

Question

I am currently studying discriminant analysis. I have encountered the phrases "likelihood-based LDA" (with some prior) and "likelihood-based QDA" (with some prior). I know what LDA (with some prior) and QDA (with some prior) are, and I have implemented them in R, but I don't understand what "likelihood-based LDA" and "likelihood-based QDA" are, how they relate to LDA and QDA (or whether they are the same concept), and how they are implemented in R (compared to the usual LDA and QDA).

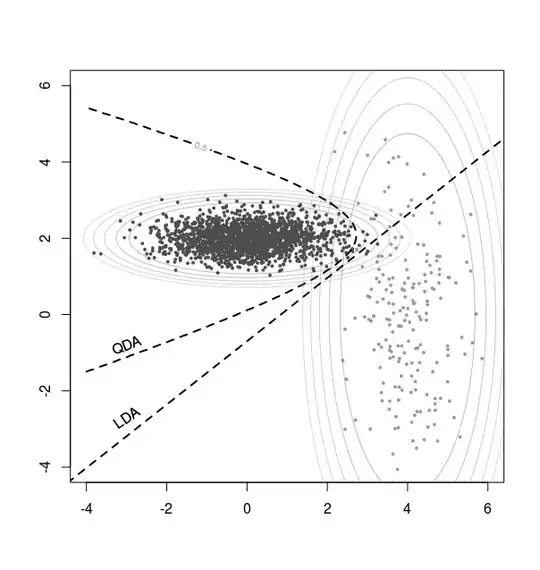
When I implemented LDA and QDA (with uniform priors over 3 classes) in R, I did the following:

lda.0 = lda( x ~ a + b + c + d + e + f, data = data, prior = c(1/3,1/3,1/3) )
preds.0 = predict( lda.0 )$class

xtabs( ~ preds.0 + data$x )

qda.0 = qda( x ~ a + b + c + d + e + f, data = data, prior = c(1/3,1/3,1/3) )
preds.0 = predict( qda.0 )$class

xtabs( ~ preds.0 + data$x )

The lda() and qda() functions are from the MASS package https://www.rdocumentation.org/packages/MASS/versions/7.3-53/topics/lda https://www.rdocumentation.org/packages/MASS/versions/7.3-53/topics/qda

What is "likelihood-based LDA" and "likelihood-based QDA", how do they relate to LDA and QDA, and how they are implemented in R (compared to the implementation above)? Links to good resources would also be appreciated.

---

This exercise statement is why I'm asking this question:

And here is the provided solution (no code provided):

---

Here are all of the relevant textbook mentions of "likelihood" for this context:

Answer 1

Functions lda() and qda() in R perform classification based on Gaussian likelihood. This means that they assume that the distribution of features (predictors) is multivariate normal in each class. The difference between lda() and qda(): LDA says that the covariance matrix is same in each class and QDA allows the covariance matrix to vary over the classes.

Generally speaking, the philosophy of LDA and QDA does not require the data to be Gaussian. Still, this is how Ronald Fisher developed LDA originally and this is how you get linearity of the boundaries separating the classes.

Answer 2

These terms likelihood-based LDA and likelihood-based QDA are not special terms for some special case or adaptation of LDA and QDA.

The likelihood-based is just an adjective to describe the LDA and QDA. It creates a pleonasm because LDA and QDA are likelihood-based (just like the algebra-based least squares method, the probability-based maximum posterior estimate, the itterative-least-squares-based generalized linear models, etc.)

LDA and QDA can be seen as based on likelihood when the distribution is multivariate Gaussian. LDA assumes equal covariance for the classes and QDA is without this assumption. These methods estimate the distribution of the classes. Then to create a classifier they compute the line (LDA) or quadratic curve (QDA) that corresponds with the likelihood-based or posterior-based (when you include prior class probabilities) naive Bayesian classifier. This line or curve passes through points where both classes are equally probable. You can see this being demonstrated for QDA in the image from this question: LDA and Fisher LDA - are their weight vectors always equivalent?

The reason why you encountered these terms likelihood-based LDA and likelihood-based QDA are not very clear. But based on your example I imagine that it might have been used to accentuate the difference with methods that are not based on likelihood.

In your example there's a question "apply the likelihood-based discriminant approach" which is followed up by an answer which ends up using the terms likelihood-based LDA and likelihood-based QDA.

The contrasting non-likelihood-based classifiers are difficult to imagine. Most estimation is in some way or another related to likelihood or posterior probability. But you could imagine methods that are approximations or heuristic, like the k-nearest neighbors algorithm.