Predictions of boosted models are sums of all the leaf weights $f_i(x)$ for some observation $x$. After $k$ rounds of boosting, the prediction $\hat{y}^{(k)}$ for a single observation is
$$
\hat{y}^{(0)} = f_0(x)\\
\hat{y}^{(1)} = \hat{y}^{(0)} + f_1(x) \\
\vdots \\
\hat{y}^{(k)} = \hat{y}^{(k-1)} + f_k(x) = \sum_{i=0}^k f_i(x)
$$
where $f_k$ is the prediction from the $k$th booster (tree). Note that $f_0$ is given ahead of time, not something learned by the xgboost model. Usually, $f_0$ is chosen to be some constant, such as the mean value of $y$.
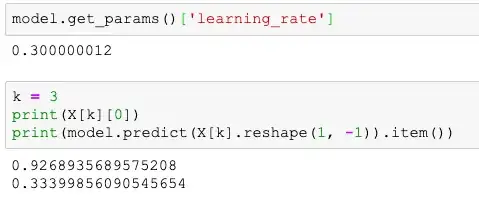
In your regression model, $f_0 = 0.5$ for every observation. We know this because the printout of the model object says base_score=0.5. For the single sample you provide, we have $f_1(x)=-0.166 \dots$. This gives a prediction of $$\hat{y}^{(1)}=0.5 -0.166 \ldots = 0.334\dots$$
The xgboost documentation has a helpful introduction to how boosting works. https://xgboost.readthedocs.io/en/latest/tutorials/model.html
Other models (most notably classification models), will often predict some transformation of the sum of the leaf weights. For example: How does gradient boosting calculate probability estimates?