Does the distribution $f(x) \propto (1-x^2)^{n/2}$ have a name?

Question

The distribution $f(x) \propto (1-x^2)^{n/2}$ for $-1 \leq x \leq 1$

• It occurs in a problem like Law of the norm of the empirical mean of uniforms on the sphere?

• It relates to intersections of high dimensional sphere. See the image from this question: Volumes of n-balls: what is so special about n=5?

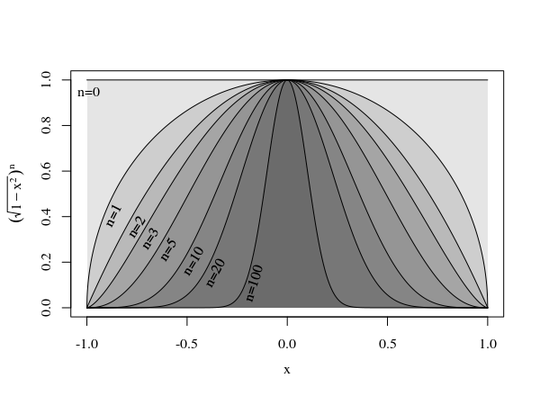
• It is the distribution of a coordinate of point that is uniform distributed on a sphere: Average absolute value of a coordinate of a random unit vector?

Answer 1

This distribution is a scaled and shifted beta distribution. This can be seen by rewriting $t=0.5+0.5x$ or $x = 2t-1$ such that $1-x^2 = 4 t(1-t)$

Answer 2

It is known as a Power semi-circle distribution with pdf $f(x)$:

$$f(x) = \frac{1}{\sqrt{\pi }}\frac{\Gamma (\theta +2) }{ \Gamma \left(\theta +\frac{3}{2}\right)} \sqrt{1-x^2}^{2 \theta +1} \quad \quad \text{for } -1 < x < 1$$

... where shape parameter $\theta > -\frac{3}{2}$, and where your parameter $n = 2 \theta + 1$.

It nests a number of known distributions including:

• ArcSine(-1,1) $\quad$ if $\theta = -1$
• Uniform(-1,1) $\quad$ if $\theta = -\frac12$
• Semicircle(-1,1) $\quad$ if $\theta = 0$
• Epanechnikov kernel $\quad$ if $\theta = \frac12$
• Bi-weight kernel $\quad$ if $\theta = \frac32$
• Tri-weight kernel $\quad$ if $\theta = \frac52$

A reference is:

Kingman, J. F. C. (1963), Random walks with spherical symmetry, Acta Mathematica, 109(1), 11-53.