First time poster, I'm looking for some assistance with parallel analysis in R. I am doing exploratory factor analysis (EFA) on a 22 item questionnaire (n=6598) and looking for an effective way to decide on an appropriate number of factors to retain. The items are on an ordinal Likert Scale from 1 to 5, so polychoric correlations are used in any factor analysis.
The code I used for my initial factor analysis was:
core_fac <- fa(core,cor='poly',fm="pa",nfactors=3,rotate='quartimin')
It is worth noting that when I look at all my eigenvalues using the following code:
core_fac$values
I get the some negative eigenvalues. That has already been its own debacle but is not the primary reason I am here.
Most of the literature I had read suggested using the Kaiser Criterion and the Scree plot test to make the decision, however, Parallel Analysis (PA) consistently came up as the most robust method for deciding the number of factors. Using the psych package, I have run the following code:
core_parr <- fa.parallel(core,
cor='poly', ## type of correlation to use
fm="pa", ## method of factor estimation
n.iter=20, ## number of simulated iterations
fa='both', ## calculate components, factors, or both
SMC=TRUE,
quant = .95, ## percentile cut off
nfactors=22) ## number of factors to extract
This gives me the following outputs:
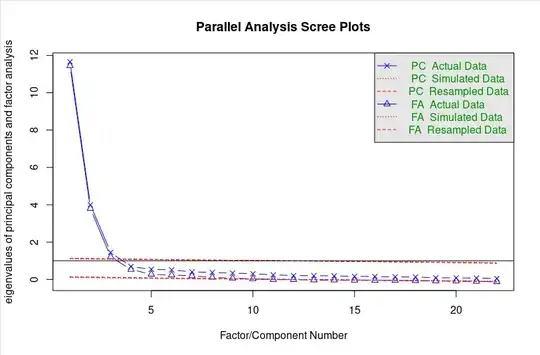
This is where I run into some issues. The eigenvalues of the simulated factors are much lower than I had anticipated, and it seems there is some conflict on which values I should be using to determine how many factors I retain. According to this paper, the Kaiser Criterion for EFA (as opposed to PCA) is actually to retain all non-negative factors. When taking this into account, low simulated eigenvalues make more sense. However, retaining 10 factors is not what I would consider desirable (and all eigenvalues are 10 are negative in my real data anyways).
However, according to this paper, "A principal components model should be used because the population matrix from which the sampled random data matrices are drawn is itself an identity matrix. In other words, the random data are free from measurement error." Using this recommendation my retained factors would instead by 3 which is much more agreeable and more in line with the current theory.
I had initially been working in SAS, but came over to R for better PA support. However, one other issue with the proposed 10-factor model, is that any model that had over 5 factors in it would generate a quasi-Heywood case where the communality of one of my items exceeded its reliability.
This has put me in a bit of a tricky spot. Looking for any suggestions for what I should do, as this is the first time I have done factor analysis of any kind.
