Dominance of truncated means

Question

If for two random variables, the truncated mean of one is always larger than the other, i.e. $E(Y|Y<x)>E(X|X<x)$ for all $x$, can we infer that $Y$ first-order stochastically dominate $X$?

Answer 1

It's an interesting idea, but the answer is no.

The problem is that these (upper) truncated means only give us information about average behavior rather than upper tail behavior -- but stochastic dominance concerns upper tail behavior (across all possible values of $x$).

To construct a counterexample, let $Y$ have a Uniform distribution on $[0,2]$ so that in terms of the indicator function $\mathscr{I},$ $$F_Y(x) = \frac{x}{2}\mathscr{I}_{[0,2]}(x) + \mathscr{I}_{(2,\infty)}(x)$$ and let $X_p$ be a mixture of a Uniform distribution on $[0,1]$ and a uniform distribution on $[1,3].$ To be specific, $p$ is some mixture weight in $[0,1]$ and

$$F_{X_p}(x) = p\,x\mathscr{I}_{[0,1]}(x) + (1-p)\left(\frac{x-1}{2}\right)\mathscr{I}_{[1,3]}(x)+ \mathscr{I}_{(3,\infty)}(x).$$

See the second figure below for an example of this function with $p=5/6.$

For $0\le x\le 2$ we may compute

$$E[Y\mid Y\le x] = \frac{1}{F_Y(x)}\int_{-\infty}^x x\,\mathrm{d}F_Y(x) = \frac{x^2/4}{x/2} = \frac{x}{2}.$$

For larger $x,$ this conditional expectation reduces to the expectation $E[Y] = 1.$

A similar computation establishes that for $0 \le x \le 1$ and $p\gt 0$

$$E[X_p \mid X_p \le x] = \frac{x}{2}$$

and for $1\lt x \le 3,$

$$E[X_p \mid X_p \le x] =\frac{1 - q/2 + (1-q)(x-1)/2}{p + (1-p)(x-1)/2}$$

where

$$q = \frac{p}{p + (1-p)(x-1)/2}.$$

Here are plots of $x\to E[X_p\mid X_p\le x]$ for various values of $p.$ Superimposed on them in black is a plot of $x\to E[Y\mid Y \le x]:$

For $p \ge 2/3,$ the plot for $Y$ is never lower than the plot for $X_p:$ that is, for all $p$ between $2/3$ and $1,$ the conditional expectation of $Y$ is never less than the conditional expectation of $X$ for any cutoff point $x.$

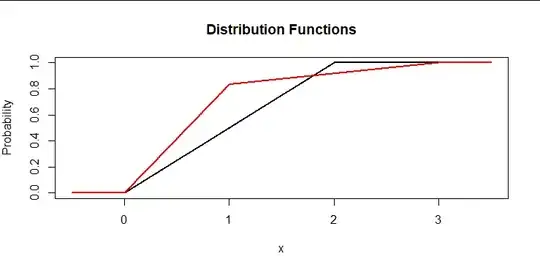
However, for $p$ in this range there is no stochastic domination of either variable. For instance, with $p=5/6$ here are plots of $F_Y$ (black) and $F_{X_p}$ (red):

One distribution dominates another only when the graph of its distribution function lies to the right of the other -- but that obviously is not the case here. That's the counterexample.