14

If I construct a 2-D matrix composed entirely of random data, I would expect the PCA and SVD components to essentially explain nothing.

Instead, it seems like the the first SVD column appears to explain 75% of the data. How can this possibly be? What am I doing wrong?

Here is the plot:

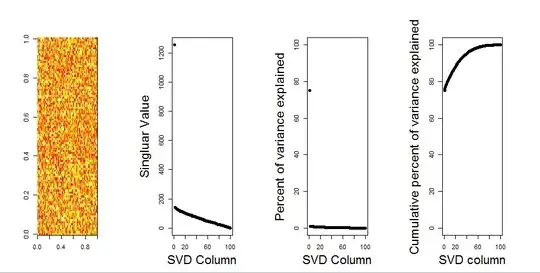
enter image description here

Here is the R code:

set.seed(1)
rm(list=ls())
m <- matrix(runif(10000,min=0,max=25), nrow=100,ncol=100)
svd1 <- svd(m, LINPACK=T)
par(mfrow=c(1,4))
image(t(m)[,nrow(m):1])
plot(svd1$d,cex.lab=2, xlab="SVD Column",ylab="Singluar Value",pch=19)

percentVarianceExplained = svd1$d^2/sum(svd1$d^2) * 100
plot(percentVarianceExplained,ylim=c(0,100),cex.lab=2, xlab="SVD Column",ylab="Percent of variance explained",pch=19)

cumulativeVarianceExplained = cumsum(svd1$d^2/sum(svd1$d^2)) * 100
plot(cumulativeVarianceExplained,ylim=c(0,100),cex.lab=2, xlab="SVD column",ylab="Cumulative percent of variance explained",pch=19)

Update

Thankyou @Aaron. The fix, as you noted, was to add scaling to the matrix so that the numbers are centered around 0 (i.e. the mean is 0).

m <- scale(m, scale=FALSE)

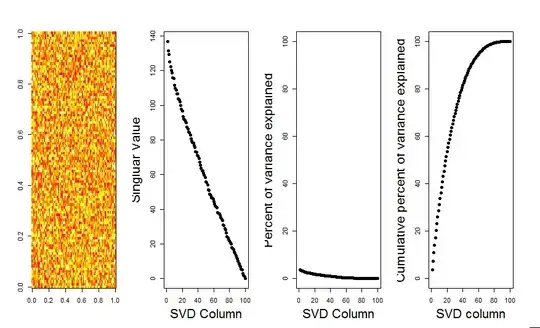
Here is the corrected image, showing for a matrix with random data, the first SVD column is close to 0, as expected.

Corrected image

Contango
  • 1,387
  • 1
  • 16
  • 15
  • 4
    Your matrix approximates a uniform distribution on the unit cube $[0,1]^{100}$ in $\mathbb{R}^{100}$. SVD computes its moments of inertia *about the origin*. In $\mathbb{R}^n$ the "total variance" must be $n$ times that of the unit interval, which is $1/3$. It is straightforward to compute that the moment along the main axis of the cube (emanating from the origin) equals $n/3-(n-1)/12$ and all the other moments--by virtue of symmetry--equal $1/12$. Therefore the first eigenvalue is $(n/3-(n-1)/12)/(n/3)=3/4+1/(4n)$ of the total. For $n=100$ that's $75.25$%, visible in the third plot. – whuber Feb 09 '13 at 21:36

2 Answers2

12

The first PC is explaining that the variables are not centered around zero. Scaling first or centering your random variables around zero will have the result you expect. For example, either of these:

m <- matrix(runif(10000,min=0,max=25), nrow=100,ncol=100)
m <- scale(m, scale=FALSE)

m <- matrix(runif(10000,min=-25,max=25), nrow=100,ncol=100)
Aaron left Stack Overflow
  • 6,808
  • 29
  • 51
  • 4
    You raise a good point, but I think this only tells a part of the story. Indeed, I would guess that the OP would try each of these and *still* be surprised by the result. The fact of the matter is that because the singular values are *ordered* in the output, they will not appear (and indeed are not) uniformly distributed as might be naively expected from "random" data. The [Marchenko-Pastur distribution](http://en.wikipedia.org/wiki/Marchenko%E2%80%93Pastur_distribution) governs their behavior in this case. – cardinal Feb 09 '13 at 19:53
  • @Aaron Thank you, you were absolutely right. I've added a graph of the corrected output above to show how the beautiful the result is. – Contango Feb 10 '13 at 10:54
  • 1
    @cardinal Thanks for your comment, you are absolutely right (see the graph produced by the corrected code, above). I believe the SVD values would become less uniformly distributed as the matrix gets smaller, as a smaller matrix would have more chance of having patterns that would not be squashed by the law of large numbers. – Contango Feb 10 '13 at 10:59
3

I'll add a more visual answer to your question, through use of a null model comparison. The procedure randomly shuffles the data in each column to preserve the overall variance while covariance between variables (columns) is lost. This is performed several times and the resulting distribution of singular values in the randomized matrix is compared to the original values.

I use prcomp instead of svd for the matrix decomposition, but the results are similar:

set.seed(1)
m <- matrix(runif(10000,min=0,max=25), nrow=100,ncol=100)

S <- svd(scale(m, center = TRUE, scale=FALSE))
P <- prcomp(m, center = TRUE, scale=FALSE)
plot(S$d, P$sdev) # linearly related

The null model comparison is performed on the centered matrix below: 

library(sinkr) # https://github.com/marchtaylor/sinkr

# centred data
Pnull <- prcompNull(m, center = TRUE, scale=FALSE, nperm = 100)
Pnull$n.sig
boxplot(Pnull$Lambda[,1:20], ylim=range(Pnull$Lambda[,1:20], Pnull$Lambda.orig[1:20]), outline=FALSE, col=8, border="grey50", log="y", main=paste("m (center=FALSE); n sig. =", Pnull$n.sig))
lines(apply(Pnull$Lambda, 2, FUN=quantile, probs=0.95))
points(Pnull$Lambda.orig[1:20], pch=16)

The following is a boxplot of the permutated matrix with the 95 % quantile of each singular value shown as the solid line. The original values of PCA of m are the dots. all of which lie beneath the 95 % line - Thus their amplitude is indistinguishable from random noise.

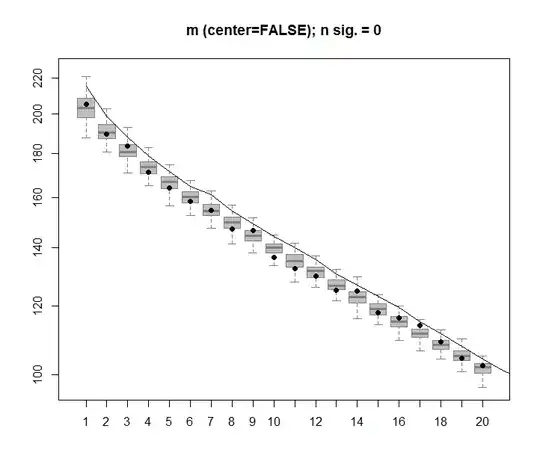
enter image description here

The same procedure can be done on the un-centred version of m with the same result - No significant singular values:

# centred data
Pnull <- prcompNull(m, center = FALSE, scale=FALSE, nperm = 100)
Pnull$n.sig
boxplot(Pnull$Lambda[,1:20], ylim=range(Pnull$Lambda[,1:20], Pnull$Lambda.orig[1:20]), outline=FALSE, col=8, border="grey50", log="y", main=paste("m (center=TRUE); n sig. =", Pnull$n.sig))
lines(apply(Pnull$Lambda, 2, FUN=quantile, probs=0.95))
points(Pnull$Lambda.orig[1:20], pch=16)

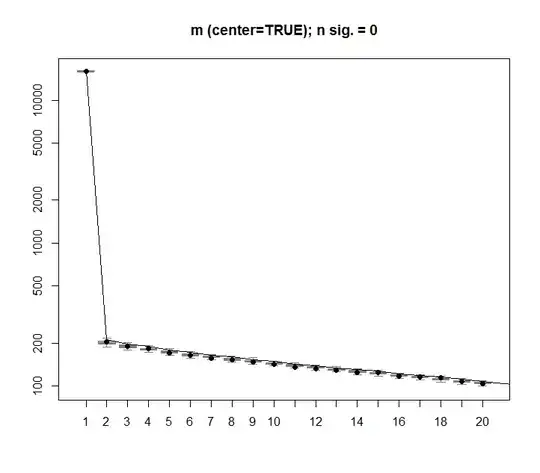
enter image description here

For comparison, let's look at a dataset with a non-random dataset: iris

# iris dataset example
m <- iris[,1:4]
Pnull <- prcompNull(m, center = TRUE, scale=FALSE, nperm = 100)
Pnull$n.sig
boxplot(Pnull$Lambda, ylim=range(Pnull$Lambda, Pnull$Lambda.orig), outline=FALSE, col=8, border="grey50", log="y", main=paste("m (center=FALSE); n sig. =", Pnull$n.sig))
lines(apply(Pnull$Lambda, 2, FUN=quantile, probs=0.95))
points(Pnull$Lambda.orig[1:20], pch=16)

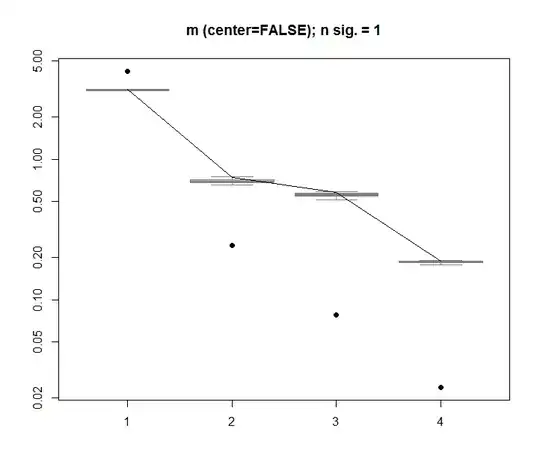
enter image description here

Here, the 1st singular value is significant, and explains over 92 % of the total variance:

P <- prcomp(m, center = TRUE)
P$sdev^2 / sum(P$sdev^2)
# [1] 0.924618723 0.053066483 0.017102610 0.005212184
Marc in the box
  • 3,532
  • 3
  • 33
  • 47
  • +1. The example of Iris dataset is interesting, because looking at the first two PCs (as e.g. in your own post here http://stats.stackexchange.com/a/88092) it is quite clear that the second one does carry some signal. The permutation (aka shuffling) test indicates that only the 1st one is "significant" though. It is clear that shuffling tends to underestimate the number of PCs: the large variance of the first real PC will get "spread out" across shuffled PCs and will elevate all of them starting from the second. One can devise more sensitive tests that account for that but this is rarely done. – amoeba Apr 10 '16 at 20:27
  • @amoeba - Excellent comment. I have been wondering about the "spreading out" effect for some time now. I suppose a cross-validation test might be one of the more sensitive ones that you reference (e.g. your answer [here](http://stats.stackexchange.com/a/85557/10675) )? Would be great if you could provide an example / reference. – Marc in the box Apr 11 '16 at 07:17
  • I usually prefer to use cross-validation (based on reconstruction error, as per [my answer here](http://stats.stackexchange.com/questions/93845)), but I am actually not sure if it is not somehow suffering from the same kind of insensitivity or not. Might make sense to try it out on the Iris dataset. Regarding the shuffling-based approaches, I don't know any reference for accounting for this "spreading out", I just know some people who were working on it recently. I think they wanted to write it up soon. The idea is to introduce some downscaling factors for the variances of higher shuffled PCs. – amoeba Apr 11 '16 at 09:12
  • @amoeba - Thanks for that link. It explains a lot for me. I found it especially interesting to see that cross validation in PCA makes use of methods that can operate on datasets with missing values. I made a few attempts on this approach and (as you state) the null model shuffling approach does indeed tend to underestimate the number of significant PCs. However, for the iris dataset, I consistently return a single PC for reconstruction error. Interesting given what you mentioned about the plot. Could be that if we were gauging error based on species predictions, results might be different. – Marc in the box Apr 11 '16 at 15:01
  • Out of curiosity, I tried it out on the Iris data. Actually, I do get two significant PCs with the cross-validation method. I updated my linked post, please see there. – amoeba Apr 12 '16 at 00:22
  • @amoeba - Thanks for that update and the code that you added. Looks like I was probably using the "Approximate method" - I will definitely try pseudoinverse approach in the future. – Marc in the box Apr 12 '16 at 06:21