Either the number of binomial trials or the number of observations will do; usually we think of this result as applying more generally than binomial data and so think of the number of observations as the $n\to\infty$.
It's also important to note that the asymptotic equivalence is local. Suppose 0 is the null value of $\theta$. If you set $\theta=\theta_A=\neq 0$ and take $n$ observations with that value of $\theta$, $n\to\infty$, there is no guarantee that the the test statistics will approach each other. The standard result is that if you take have a sequence values $\theta_n=h/\sqrt{n}$ and take $n$ observations with $\theta=\theta_n$, then as $n\to\infty$ the score, Wald, and likelihood ratio tests will converge in probability to the same random variable.
Here's the picture: on a graph with the score (derivative of loglikelihood) on the $y$-axis and $\theta$ on the $x$-axis, the Wald chi-squared statistic is twice the area of the blue triangle. The score chi-squared statistic is twice the area of the red triangle, and the likelihood ratio chi-squared statistic is twice the grey area under the curve.
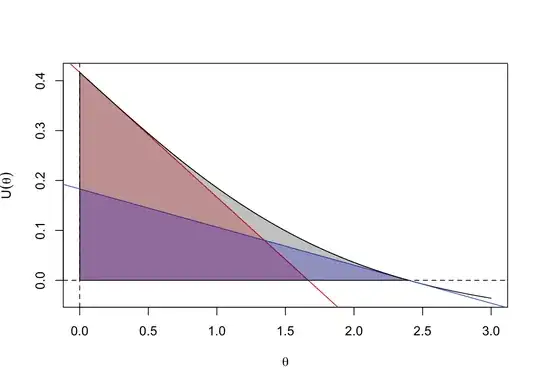
With $n\to\infty$ and $\theta_n=h/\sqrt{n}$, we're zooming in to this picture. The curve locally asymptotically approaches a straight line and the three coloured areas become the same
But if you fix $\theta\neq 0$ and just increase $n$, the picture doesn't change. It still just looks like
 and there's no asymptotic equivalence.
and there's no asymptotic equivalence.


