Currently I am re-reading some chapters of: An Introduction to Statistical Learning with Applications in R by Gareth James, Daniela Witten, Trevor Hastie and Robert Tibshirani (Springer, 2015). Now, I have some doubts about what is said there.
Above all it seems to me relevant to note that in chapter 2 two concepts are introduced : prediction accuracy-model interpretability tradeoff and bias-variance tradeoff. I mentioned the latter in an earlier question.
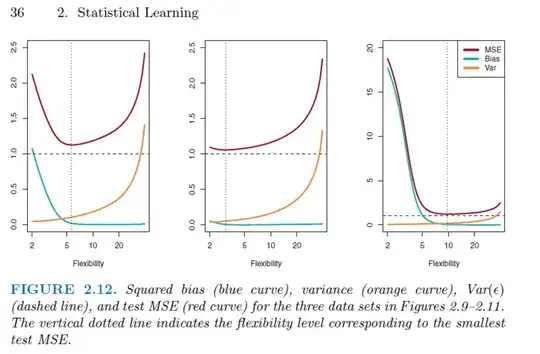
In this book, it is suggested that focusing on expected prediction error (test MSE) yields the following assertions:
less flexible specifications imply more bias but less variance
more flexible specifications imply less bias but more variance
It follows that linear regression implies more bias but less variance. The optimum in the tradeoff between bias and variance, the minimum in test MSE, depends on the true form of $f()$ [in $Y = f(X) + \epsilon$]. Sometimes linear regression works better than more flexible alternatives and sometimes not. This graph tells this story:
In the second case linear regression works quite well, in the others two not so much. All is ok in this perspective.
In my opinion the problem appears under the perspective of inference and interpretability used in this book. In fact this book also suggests that:
less flexible specifications are more far away from reality, then more biased, but at the same time they are more tractable and, then, more interpretable;
more flexible specifications are closer to the reality, hence less biased, but at the same time they are less tractable and, then, less interpretable.
As a result we have that linear regressions, OLS and even more LASSO, are the most interpretable and more powerful for inference. This graph tell this story:
This seems to me like a contradiction. How is possible that linear models are, at the same time, the more biased but the best for inference? And among linear models, how is possible that LASSO regression is better than OLS one for inference?
EDIT: My question can summarized as:
linear estimated model are indicated as the more interpretable even if the more biased.
linear estimated model are indicated as the more reliable for inference even if the more biased.
I read carefully the answer and comments of Tim. However it seems to me that some problems remain. So, actually it looks like in some sense the first condition can hold, i.e. in a sense where “interpretability” is a property of the estimated model itself (its relation with something "outside" are not considered).
About inference "outside" is the core, but the problem can move around its precise meaning. Then, I checked the definition that Tim suggested (What is the definition of Inference?), also here (https://en.wikipedia.org/wiki/Statistical_inference), and elsewhere. Some definition are quite general but in most material that I have inference is intended as something like: from sample say something about the "true model", regardless of his deep meaning. So, the Authors of the book under consideration used something like the “true model”, implying we cannot skip it. Now, any biased estimator cannot say something right about the true model and/or its parameters, even asymptotically. Unbiasedness/consistency (difference irrelevant here) is the main requirements for any model written for pure inference goal. Therefore the second condition cannot hold, and the contradiction remains.