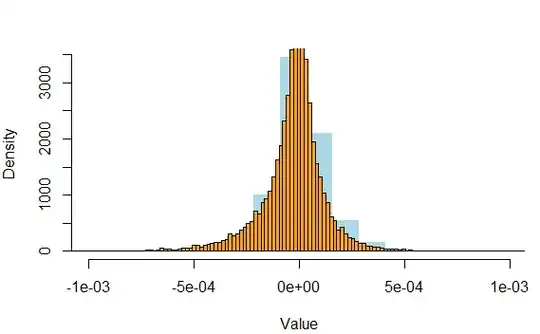
I'm trying to fit Variance-Gamma distribution to empirical data of 1-minute logarithmic returns. In order to visualize the results I plotted together 2 histograms: empirical and theoretical. ('a' is a vector of empirical data):
SP_hist<-hist(a,col="lightblue",freq=FALSE,breaks = seq(min(a),max(a),length.out = 141), border="white",main="", xlab="Value",xlim=c(-0.001,0.001)) hist(VG_sim_rescaled,freq=FALSE,breaks=seq(min(VG_sim_rescaled),max(VG_sim_rescaled),length.out = 141),xlab="Value",main="",col="orange",add=TRUE)
(empirical histogram - blue, theoretical histogram-orange)
However,after having plotted 2 histograms together, I started wondering about 2 things:
- In both histograms I stated, that freq=FALSE. Therefore, the y-axis should be in range (0,1). In the actual picture values on the y-axis exceed 3000. How could it happen? How to solve it?
- I need to change the bucketing size (the width of the buckets) and the density per unit length of the x-axis. How is it possible to do these tasks?
Besides, how is it possible to use any statistical tests to prove the goodness-of-fit of the Variance-Gamma distribution to a given set of empirical data? I've tried to use chisq.test(a,VG_sim_rescaled), but when I run this code, RStudio stops reacting on my commands and soon switches off. Maybe it's caused by extremely long vectors, which are given to chisq.test() (each of them contains about 16000 values).
Thank you for your help.