I am trying to reason about the following scenario:
Let us have three random variables: $X$, $Y$, $Z$. $Y$ is independent of $Z$. Let us also have the following CDF's:
$$F_X, F_{X \mid Y}, F_{X \mid Z}$$
With the relationships:
$$F_X \neq F_{X \mid Y}\neq F_{X \mid Z}$$
I am trying to reason about what we can expect $F_{X \mid Y, Z}$ to be, given the above information. My intuition (and this was suggested in a comment here) is that $F_{X \mid Y, Z}$ can be expected to a be a weighted average of $F_{X \mid Y}$ and $F_{X \mid Z}$:
$$F_{X \mid Y, Z} = 0.5F_{X \mid Y} + 0.5F_{X \mid Z}$$
The reasoning for this is that if both $Y$ and $Z$ affect $X$, then knowing that both $Y$ and $Z$ occurred it seems reasonable to expect the total affect on $X$ to be partly due to $Y$ and partly due $Z$. Even though this seems reasonable, I have not been able to find a source/any derivation that this is indeed correct reasoning (hence this question).
Example
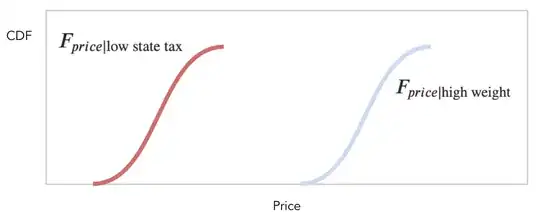
An example may make this more concrete. Consider the scenario where we are trying to model shipping prices. Let $X$ be price, $Y$ be weight and $Z$ be state tax. We are given that weight and state tax are independent of each other (i.e. the weight of a shipment does not affect the state tax that it is being shipped to). We also are given that weight affects price (heavier objects cost more to ship), and state tax affects price (different states cost more or less to ship to). Let us now be given that the object we are trying to ship has a high weight and a state with low tax. Our CDF's $F_{price \mid \text{high weight}}$ and $F_{price \mid \text{low state tax}}$ then look like:
Where we can see clearly (as you would expect) that $F_{price \mid \text{high weight}}$ is shifted to the right compared to $F_{price \mid \text{low state tax}}$ (i.e. it has a higher average price).
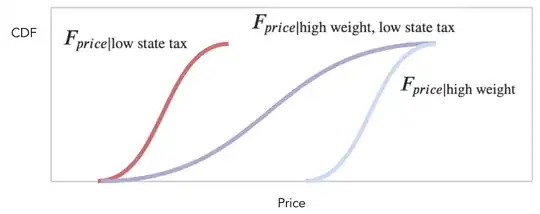
Now let us consider how $price$ responds when we know both we have a low state tax and a high weight. Intuitively it seems as though we would expect our price to be increased due to the high weight, and decreased due to the low tax, meaning our price would be a weighted average in essence.
This would like like:
$$F_{price \mid \text{high weight, low state tax}} = 0.5F_{price \mid \text{low state tax}} + 0.5F_{price \mid \text{high weight}}$$
Where visually we can see $F_{price \mid \text{high weight, low state tax}}$ is a weighted average of $F_{price \mid \text{low state tax}}$ and $F_{price \mid \text{high weight}}$:
Subsequently, if we observe that $F_{price \mid \text{high weight, low state tax}}$ is actually far different than $0.5F_{price \mid \text{low state tax}} + 0.5F_{price \mid \text{high weight}}$, we can conclude that their is some interaction occurring (for instance maybe shipments of a high weight get an additional tax when shipped to this particular state, hence shifting our CDF $F_{price \mid \text{high weight, low state tax}}$).
Additional Resources
For anyone interested, I have read through the following related posts, but none have quite answered the question I am posting here.