0

I am trying to determine if wildfires occur closer to forests or not. For this, I have two matrices with the same shape:

  1. A matrix of ones and zeros where each value represents whether a fire is present or not.
  2. A matrix where each value represents the distance to the nearest forest. As this was derived from another matrix that represented forest areas, all the distances are integers starting from zero.

Following the approach of Kumar et al. (2014), I extracted two different groups of distances to compare:

  1. The distances where a fire occured (N = 2407).
  2. All the distances in the study area (N = 58544).

and ran a two-sample Kolmogorov-Smirnov test to check whether the two groups of distances belong to the same distribution.

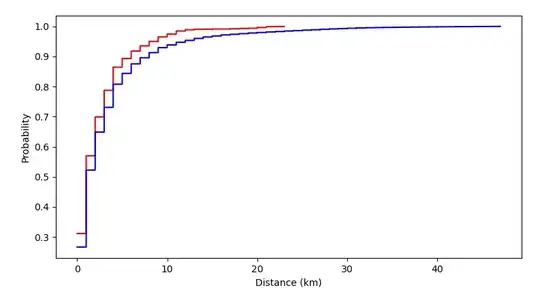
For some context, here is a plot with the ECDFs of the first group of distances (red) and the second (blue).

enter image description here

Should anyone would want to access the data and reproduce the test, here is a link to download it and a small R snippet to load it:

> all <- scan("all.txt")
> fire <- scan("fire.txt")

I got the following result for the Kolmogorov-Smirnov test:

> ks.test(fire, all)

    Two-sample Kolmogorov-Smirnov test

data:  fire and all
D = 0.056674, p-value = 7.098e-07
alternative hypothesis: two-sided

Warning message:
In ks.test(fire, all) : p-value will be approximate in the presence of ties

My interpretation, taking a look at the small p-value, is that the test suggests that both groups of distances belong to different distributions. However, the D statistic relatively small, suggesting that they might belong to the same distribution after all. Also, given the nature of the data, there are many ties. I'm wondering if there is a better approach to achieve my objective.

I took a look at a similar question and one of the answers suggests using a Chi-Squared test. As the groups of distances do not share the same size (N), I'd think this is not a possibility.

Furthermore, I have other study areas and in some cases the distributions seem to match, in other fires appear to occur closer to the forest and in other fires appear to occur farther from the forests. Is there any test that can statistically tell me whether the distributions are "smaller" (closer), "larger" (farther) or similar?

Marcelo Villa-Piñeros
  • 71
  • 7
  • How are all the distances related in the study area? For example, if the study area is a gird of 1 acre plots of land, then two adjacent grid locations are not likely to be independent, and this would bias your results. I'm thinking there may be a way to use blocking or sampling to improve the design of this test. – jeffalltogether Aug 22 '20 at 04:34
  • The grid is composed of 1km pixels. Imagine we divided the US in a 1km grid and for each pixel we calculated the distance to the nearest forest. – Marcelo Villa-Piñeros Aug 22 '20 at 14:22
  • We deal with this in image data. Neighboring pixels from the same image are not independent. Therefore we would produce one statistic from a single image and then compare it to other images where each image was iid. In your case you might be able to apply a sampling technique like hierarchical or cluster sampling to get iid measurements from your grid. – jeffalltogether Aug 22 '20 at 16:07
  • I have an image for a specific period of time. If I applied one of the sampling techniques you mention, how would I compare the samples? Seems like a 2 sample Kolmogorov-Smirnov test is not the most appropiate in this case. Feel free to elaborate in an answer if you have the time. – Marcelo Villa-Piñeros Aug 22 '20 at 22:33

1 Answers1

1

After thinking about this a bit I would propose the following:

1 - simply plot a histogram to see if fires are occurring closer to forests. Looking at the shape would be a first sniff-test.

2 - if the histogram is suggesting the pattern is present, then I would be asking, “is this coincidence or real?”. My biggest question is from the fact that not all parcels of land are created equally. I would want to also look at other questions like:

  1. How much vegetation is on the land;
  2. Is there a road on the land where someone could throw a lit cigarette out their car window; and
  3. Etc.

If you don’t have this info, but you have a picture, you could simply use RGB values as surrogates.

Then, I would throw all those variables into a logistic regression. With y being fire/no fire and X’s being the predictor variables including distance the the nearest forest. You might want to look into a GLMM where image could be the random effect.

If the coefficient on distance looks reasonably significant, then you’re looking good and you have controlled for some confounding covariates.

Now, the probability of fire as a function of distance to a forest may not be linear. But I still think the regression approach would be reasonable.

This is just my 2 cents on an approach. Hope this helps with your project!

jeffalltogether
  • 534
  • 4
  • 12