Non-significant ANOVA interaction term despite 95% confidence intervals not overlapping

Question

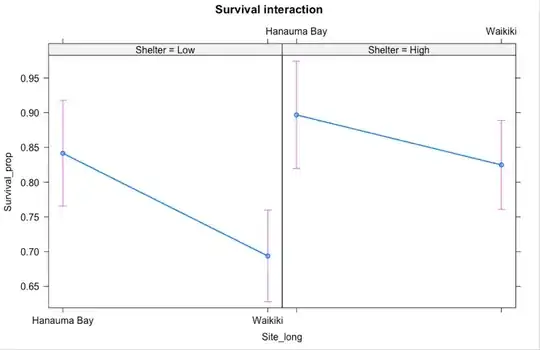
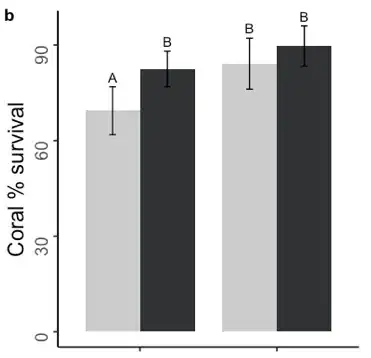
I plotted the means and 95% confidence intervals for survival data with the paired bars corresponding to 2 different study sites that each contain two experimental treatments (white = low shelter, black = high shelter). As you can see for the Waikiki site (bars on the left), the 95% CI do not overlap as confirmed by the upper and lower limits that define the error bars in the summary dataframe below.

However, when I run the mixed model for these data, the Site_long x Shelter term is not significant despite the confidence intervals in the figure.

Linear mixed model fit by REML. t-tests use Satterthwaite's method ['lmerModLmerTest']
Formula: Survival_prop ~ Site_long * Shelter + (1 | Season) + (1 | Year)
   Data: survival_results_long_2

REML criterion at convergence: 21.7

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.6051 -0.5895  0.3570  0.6512  1.4160 

Random effects:
 Groups   Name        Variance Std.Dev.
 Season   (Intercept) 0.001181 0.03437 
 Year     (Intercept) 0.002929 0.05412 
 Residual             0.058588 0.24205 
Number of obs: 194, groups:  Season, 4; Year, 3

Fixed effects:
                            Estimate Std. Error        df t value Pr(>|t|)    
(Intercept)                  0.88820    0.04549   3.74510  19.524 6.62e-05 ***
Site_longWaikiki            -0.11677    0.03537 186.17978  -3.301  0.00115 ** 
Shelter.L                    0.03558    0.03813 186.39549   0.933  0.35191    
Site_longWaikiki:Shelter.L   0.05540    0.04992 185.81545   1.110  0.26852    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
            (Intr) St_lnW Shlt.L
Site_lngWkk -0.462              
Shelter.L    0.008 -0.010       
St_lngW:S.L -0.008 -0.003 -0.764

Is the correct interpretation to say that since the 95% CI bars don't overlap AND the Tukey pairwise multiple comparisons confirm that the means for Waikiki-Low (white bar on left) and Waikiki-High (black bar on left) shelter treatments are significantly different that this interaction is significant despite the model results?

contrast                           estimate     SE  df t.ratio p.value
 Hanauma Bay Low - Waikiki Low        0.1559 0.0501 186  3.111  0.0115 
 Hanauma Bay Low - Hanauma Bay High  -0.0503 0.0541 187 -0.930  0.7887 
 Hanauma Bay Low - Waikiki High       0.0273 0.0497 186  0.549  0.9467 
 Waikiki Low - Hanauma Bay High      -0.2063 0.0505 186 -4.083  0.0004 
 Waikiki Low - Waikiki High          -0.1287 0.0456 185 -2.823  0.0269 
 Hanauma Bay High - Waikiki High      0.0776 0.0501 187  1.550  0.4100 

For completeness, I have also provided the model outputs for the simple linear model with and without the interaction term between Site and Shelter:

Simple linear model with interaction term

Call:
lm(formula = Survival_prop ~ Site_long * Shelter, data = survival_results_long_2, 
    na.action = "na.fail")

Residuals:
    Min      1Q  Median      3Q     Max 
-0.8967 -0.1581  0.1033  0.1584  0.3062 

Coefficients:
                           Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 0.86915    0.02748  31.631   <2e-16 ***
Site_longWaikiki           -0.10989    0.03601  -3.052   0.0026 ** 
Shelter.L                   0.03899    0.03886   1.003   0.3169    
Site_longWaikiki:Shelter.L  0.05364    0.05092   1.053   0.2935    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2473 on 190 degrees of freedom
Multiple R-squared:  0.08609,   Adjusted R-squared:  0.07166 
F-statistic: 5.966 on 3 and 190 DF,  p-value: 0.0006584

Simple linear model without the interaction term

Call:
lm(formula = Survival_prop ~ Site_long + Shelter, data = survival_results_long_2, 
    na.action = "na.fail")

Residuals:
     Min       1Q   Median       3Q      Max 
-0.91909 -0.14268  0.08091  0.18023  0.28998 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)       0.86943    0.02748  31.634  < 2e-16 ***
Site_longWaikiki -0.10974    0.03602  -3.047  0.00264 ** 
Shelter.L         0.07023    0.02512   2.796  0.00571 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2473 on 191 degrees of freedom
Multiple R-squared:  0.08076,   Adjusted R-squared:  0.07113 
F-statistic:  8.39 on 2 and 191 DF,  p-value: 0.0003219

All input is appreciated thank you!

Answer 1

There are a few things going on here. First, non-overlap of 95% confidence intervals (CI) is generally much more stringent than is required for a significant difference between two means. This answer shows that under reasonable conditions such non-overlap is equivalent to about p < 0.005 for the difference in means. There is little question for example that there is a difference between high shelter and low shelter at the Waikiki site.

Second, as a comment on an earlier version of this answer states:

When removing the interaction, both Site and Shelter come out significant ...

That argues that the anomaly isn't so much with the Waikiki site as with the Hanauma site. With an overall difference between high shelter and low shelter in the model without an interaction, one might expect to find a shelter difference for the Hanauma site, too. You don't see that in the evidently raw data in the bar plots and the first table. Raw data comparisons, however, aren't the same thing as comparing coefficients in regression models.

One point of a linear model is to share information about the underlying error terms among all of the conditions. That makes it possible to see differences that are hidden because of random variation within individual combinations of conditions, like the high shelter versus low shelter values at Hanauma. If the model had stopped at that point, one could have analyzed estimated marginal means in a way that would presumably show significant (high shelter - low shelter) differences for both Waikiki and Hanauma, both differences equal to the regression coefficient for Site in the additive model without the interaction.

Third, adding the interaction term is an attempt to look for further differences in the Shelter effect between the two sites. The interaction term isn't just looking at whether high shelter and low shelter differ at Waikiki. It's looking at whether that difference differs from the difference seen at Hanauma. That's both a mouthful to say and a lot to think about, but understanding interactions requires a lot of careful thought. That interaction term--the difference between the differences--isn't even displayed in the bar plot or the first table.

In this case, adding the interaction effect loses the apparent overall "significance" of Shelter while not providing a "significant" interaction term. That result suggests that there simply aren't enough data to support the search for the interaction term. I suspect that an ANOVA test between the models with and without the interaction would have been non-significant, in which case the data would be most efficiently and accurately represented by the additive model.

This type of behavior can be seen in situations in which some of the effects are on the borderline of significance. That seems to be the case here for the overall Shelter effect in the additive model. Then the attempt to break down the Shelter effect into separate effects for the two sites with the interaction, plus the loss of a degree of freedom for the statistical tests, ends up confusing more than clarifying.

With these data, I'd recommend just sticking with the additive model if possible. If your original hypothesis specifically included the interaction, you simply didn't collect enough data to decide on that. Then it might make sense to show results for both the additive and the interaction model.

Finally, do pay attention to the structure of the random-effects parts of the model, as noted in a comment. And if these are percentage survival values you perhaps shouldn't be using a standard linear regression as this seems to be, although in some circumstances (e.g., with limited probability ranges far enough on average from the limits of 0 and 1) such a linear probability model can sometimes be good enough.