Generating uniform points inside an $m$-dimensional ball

Question

The present question follows on from some other questions on this site asking how to generate uniform points inside a disc (see e.g., here, here and here). The natural extension of that problem is to generate points inside an $m$-dimensional ball with centre $\mathbf{c} \in \mathbb{R}^m$ and radius $r \geqslant 0$. That is, we want to generate IID random variables from the following distribution:

$$\mathbf{X} \sim \text{U}(\mathcal{B}(\mathbf{c},r)) \quad \quad \quad \mathcal{B}(\mathbf{c},r) \equiv \Big\{ \mathbf{x} \in \mathbb{R}^m \Big| ||\mathbf{x} - \mathbf{c}|| \leqslant r \Big\}.$$

How do we generate IID uniform points on this space? Is there a simple way to program this?

Answer 1

A simple and efficient method for this problem uses a variation of the well-known Box-Mueller transform, which connects the normal distribution to the uniform distribution on a ball. If we generate a random vector $\mathbf{Z} = (Z_1,...,Z_m)$ composed of IID standard normal random variables and a random variable $U \sim \text{U}(0,1)$ (independent of the first random vector) then we can construct the uniform point of interest as:

$$\mathbf{X} = \mathbf{c} + r \cdot U^{1/m} \cdot \frac{\mathbf{Z}}{||\mathbf{Z}||}.$$

In the code below we create an R function called runifball which implements this method. The function allows the user to generate n random vectors that are points on a ball with arbitrary centre, radius and dimension.

runifball <- function(n, centre = 0, center = centre, radius = 1) {
  
  #Check inputs
  if (!missing(centre) && !missing(center)) {
  if (sum((centre - center)^2) < 1e-15) { 
                 warning("specify 'centre' or 'center' but not both") } else {
                    stop("Error: specify 'centre' or 'center' but not both") } }
  if (radius < 0) { stop("Error: radius must be non-negative") }
  
  #Create output matrix
  m   <- length(center)
  OUT <- matrix(0, nrow = m, ncol = n)
  rownames(OUT) <- sprintf("x[%s]", 1:m)
  
  #Generate uniform values on circle
  UU  <- runif(n, min = 0, max = radius)
  ZZ  <- matrix(rnorm(n*m), nrow = m, ncol = n)
  for (i in 1:n) {
    OUT[, i] <- center + radius*UU[i]^(1/m)*ZZ[, i]/sqrt(sum(ZZ[, i]^2)) }
  
  OUT }

Here is an example using this function to generate random points uniformly over a two-dimensional disk. The plot shows that the points are indeed uniform over the specified ball.

#Generate points uniformly on a disk
set.seed(1)
n      <- 10^5
CENTRE <- c(5, 3)
RADIUS <- 3
UNIF   <- runifball(n, centre = CENTRE, radius = RADIUS)

#Plot the points
plot(UNIF, 
     col = rgb(0, 0, 0, 0.05), pch = 16, asp = 1,
     main = 'Points distributed uniformly over a circle', xlab = 'x', ylab = 'y')
points(x = CENTRE[1], y = CENTRE[2], col = 'red', pch = 16)

Answer 2

The simplest and least error-prone approach - for low dimensions (see below!) - would still be rejection sampling: pick uniformly distributed points from the $m$-dimensional hypercube circumscribing the sphere, then reject all that fall outside the ball.

runifball <- function(n, centre = 0, center = centre, radius = 1) {
  
  #Check inputs
  if (!missing(centre) && !missing(center)) {
  if (sum((centre - center)^2) < 1e-15) { 
                 warning("specify 'centre' or 'center' but not both") } else {
                    stop("Error: specify 'centre' or 'center' but not both") } }
  if (radius < 0) { stop("Error: radius must be non-negative") }

  n_to_generate <- 2^length(center)*gamma(length(center)/2+1)*n/pi^(length(center)/2) # see below
  
  original_sample_around_origin <- 
      matrix(replicate(length(center),runif(n_to_generate ,-radius,radius)),nrow=n_to_generate )
  index_to_keep <- rowSums(original_sample_around_origin^2)<radius^2
  original_sample_around_origin[index_to_keep,]+
      matrix(center,nrow=sum(index_to_keep),ncol=length(center),byrow=TRUE)
}

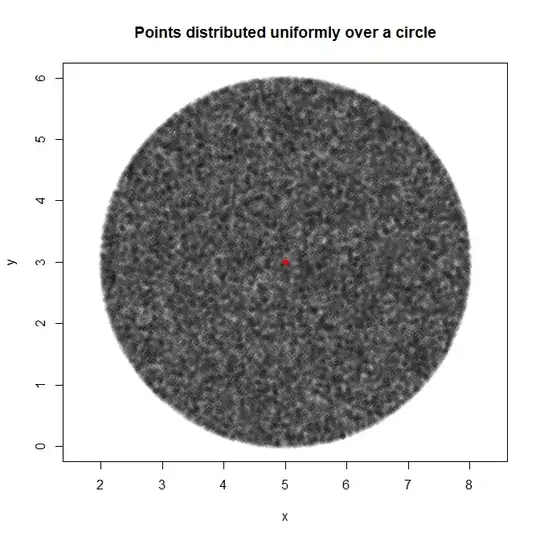
Here is an application for the $m=2$-dimensional disk:

#Generate points uniformly on a disk
set.seed(1)
n      <- 10^5
CENTRE <- c(5, 3)
RADIUS <- 3
UNIF   <- runifball(n, centre = CENTRE, radius = RADIUS)

#Plot the points
plot(UNIF, 
     col = rgb(0, 0, 0, 0.05), pch = 16, asp = 1,
     main = 'Points distributed uniformly over a circle', xlab = 'x', ylab = 'y')
points(x = CENTRE[1], y = CENTRE[2], col = 'red', pch = 16)

Once again, we will need to originally generate more points, because we will reject some. Specifically, we expect to keep $\frac{\pi^\frac{m}{2}}{2^m\Gamma(\frac{m}{2}+1)}$, which is the ratio of the volume of the $m$-dimensional ball to the volume of the $m$-dimensional hypercube circumscribing it. So we can either start by generating $\frac{2^m\Gamma(\frac{m}{2}+1)n}{\pi^\frac{m}{2}}$ and expect to end up with $n$ points (this is the approach the code above takes), or just start generating until we have kept $n$.

In either case, the number of points we originally need to draw in the hypercube in order to (expect to) end up with a single point in the ball rises quickly with increasing dimensionality $m$:

(Note the logarithmic vertical axis!)

m <- 2:20
plot(m,2^m*gamma(m/2+1)/pi^(m/2),type="o",pch=19,log="y",
    xlab="Dimension (m)")

This is just a consequence of the fact that for large $m$, most of the volume of the $m$-dimensional hypercube is in the corners, not in the center (where the ball is). So rejection sampling is likely only an option for low dimensions.