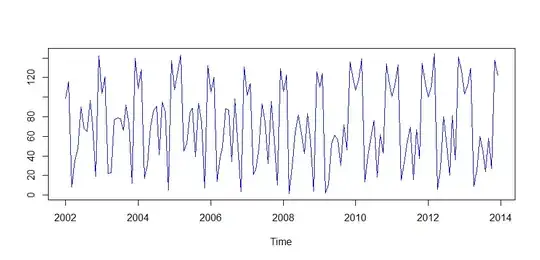
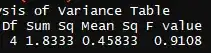
This is the current data I have
I want to know if fixed factor A has any effect on C. That is, if A1 = A2 = ... = A5.
I think I am trying to find a group difference, correct me if I am wrong.
because I read a paper saying it is fine to treat Likert scale in parametric, I changed factor C into numeric., and I decided to use mixed-effects model through
library(lme4)
library(lmerTest)
model <- lmer(C ~ A + (1|B), data)
summary(model)
anova(model)
and reached the conclusion: we cannot reject the idea that factor A is consistent in manner of variability in resultC.
Then I read about the controversies behind p-values in mixed model, then eventually question whether that p-value actually represents my question, or if it answers a completely different question.
If I want to answer my question of A1 = A2 = ... = A5, is my use of a mixed model correct?
Thank you for your guidance.